FullSimplify used with Assuming giving unexpected results

Question

Can someone shed some light on why

Assuming[{x ∈ Reals}, x (Sign[x]^2 - 1)] // FullSimplify

returns

x (-1 + Sign[x]^2)

instead of zero please?
I know one can not expect FullSimplify to perform miracles but this example does seem pretty obvious.

Answer 1

Your example evaluates

Assuming[{x ∈ Reals}, x (Sign[x]^2 - 1)]

BEFORE simplifying.

The correct way to inform your assumptions to FullSimplify[] is:

FullSimplify[x (Sign[x]^2 - 1), Assumptions -> {x ∈ Reals}] 

Which returns zero.

Or

Assuming[{x ∈ Reals}, FullSimplify[x (Sign[x]^2 - 1)]]

Answer 2

1. The first reason is that Sign[0] yields 0, so even assuming x ∈ Reals this expression:
Sign[x]^2 - 1 cannot be evaluated to 0.

2. The next problem is that Assuming[{x ∈ Reals}, x (Sign[x]^2 - 1)] is evaluated first, then the assumption imposed doesn't affect the simplification procedure since FullSimplify being outside Assuming doesn't know anything about x, thus the final result is correct.

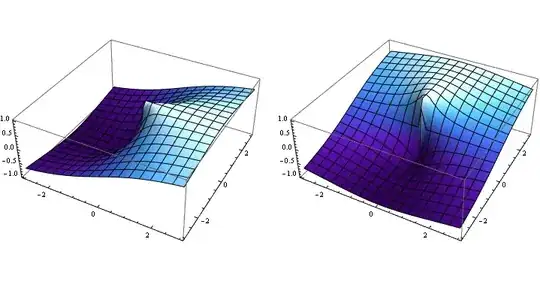
Ad 1. In general Sign is a complex function, for a complex number $ z\neq0\;$ it is equal to z/Abs[z], e.g. see its graphs of the real and imaginary parts:

GraphicsRow[ Table[ Plot3D[ f @ Sign[x + I y], {x, -3, 3}, {y, -3, 3}, 
                            ColorFunction -> "DeepSeaColors",], {f, {Re, Im}}]]

Ad.2

One can impose global assumptions for a Mathematica session, e.g.

$Assumptions = z ∈ Reals;

then one can do as it was assumed in the question:

z (Sign[z]^2 - 1) // FullSimplify

0

On the other hand you can use assumption restricted to FullSimplify only:

FullSimplify[ x (Sign[x]^2 - 1), x ∈ Reals]

0

For more detailed discussion see e.g. this question How to specify assumptions before evaluation?.