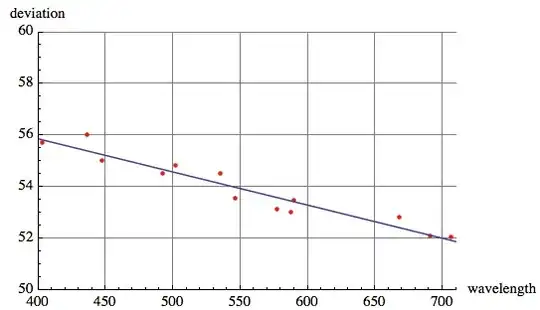
This is what I have done so far. The points are of angles-of-deviation and wavelengths from my physics lab experiment.
V = ListPlot[
{{589.3, 53.50}, {435.8, 56.02}, {535.4, 54.52}, {546.1,
53.57}, {577.0, 53.13}, {690.9, 52.10}, {402.6, 55.72}, {447.2,
55.02}, {492.2, 54.53}, {501.6, 54.83}, {587.6, 53.03}, {667.8,
52.83}, {706.5, 52.05}
}, PlotRange -> {{400, 710}, {50, 60}},
AxesLabel -> { wavelength, deviation}, PlotStyle -> Red,
GridLines -> Automatic]

I am trying to find the best fit line of these points. I know it is some type of exponential function. But I can not figure out how to do it. Please help me out.