3

I have read in some places about the errors associated with FindRoot, but the closest thing I can find on this website seems to be due to the imaginary unit. I am dealing with what should be a relatively simple function for Mathematica to handle, namely a sum of Bessel functions of the first and modified first kinds. My code is

Zeros[z_] = (BesselJ[0, z] - BesselJ[2, z])*(3*BesselI[1, z] + 
  BesselI[3, z]) - (BesselI[0, z] + 
  BesselI[2, z])*(3*BesselJ[1, z] - BesselJ[3, z]);
FindRoot[Zeros[z]==0,{z,1}]

which returns 1.4371. But Zeros[1.4371]=-2.0754. I can also find roots by looking at the graph and basically bisecting by hand. My question is, should I rely on the plot, or the findroot algorithm? I am very familiar with Newton's Method (which is what I think FindRoot uses), but it does not make sense to me how it could guess such an erroneous root; this section of the plot shows none of the typical pitfalls of Newton's method. The second root on the other hand is at ~4.4, which the FindRoot algorithm finds to be 4.77493, which isn't a bad estimate given the slope of the function at this location.

So, I guess my question boils down to, should I check (and believe) the plot or the FindRoot algorithm, or perhaps neither?

Jeremy Upsal
  • 336
  • 1
  • 9
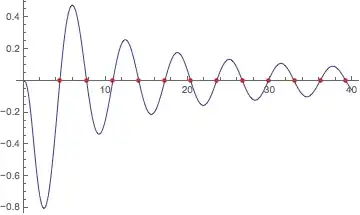
  • What version are you using? With 9.0.1, I get something approximately 0 for FindRoot[Zeros[z] == 0, {z, 1}] and 4.43216 for FindRoot[Zeros[z] == 0, {z, 4}], both of which appear to be correct. – rm -rf Nov 14 '13 at 03:36
  • I am using 9.0.0, this may be the difference. I found both of those roots by looking at the plot. Can you do me a favor and tell me what root you find near 23? There should be one at about 23.504 according to the plot. If you get this then I will update to 9.0.1 and try again, if not, I will just stick to checking out the plot. – Jeremy Upsal Nov 14 '13 at 03:57
  • 2
    I get 24.5046 for that. Can't reproduce the issue in 8.0.4 or 9.0.1. Definitely update to 9.0.1, there have been a number of bugfixes. – Szabolcs Nov 14 '13 at 05:04
  • Thank you, I think my question has been answered sufficiently now. – Jeremy Upsal Nov 14 '13 at 16:54

1 Answers1

4

I suppose you have tried your code from a fresh kernel -- sometimes old definitions unexpectedly cause such problems.

I find I get the same (correct) approximate zeros from FindRoot in V9.0.1 and V8.0.4. Here's a nice way to get a bunch of zeros using a quick but somewhat sloppy NDSolve to seed FindRoot. (It misses the easy one, z -> 0, though because WhenEvent requires a zero-crossing.)

(zeros = First @ Last @ Reap @ Quiet @ NDSolve[
   {y'[x] == Zeros'[x], y[0] == Zeros[0], 
    WhenEvent[y[x] == 0, Sow[FindRoot[Zeros[z], {z, x}]]]}, 
   y, {x, 0, 40}, AccuracyGoal -> 1, PrecisionGoal -> 1]) // AbsoluteTiming

(* {0.075423,
    {{z -> 4.43216}, {z -> 7.68556}, {z -> 10.8744}, {z -> 14.0424},
     {z -> 17.2009}, {z -> 20.3543}, {z -> 23.5046}, {z -> 26.6528},
     {z -> 29.7997}, {z -> 32.9456}, {z -> 36.0907}, {z -> 39.2353}}} *)

Plot[Zeros[z]/E^z, {z, 0, 40},
  Mesh -> {z /. zeros}, MeshStyle -> {PointSize@Medium, Red}]

Mathematica graphics

One can also use just NDSolve, but it's slower:

(zeros = First @ Last @ Reap @ Quiet @ NDSolve[
   {y'[x] == Zeros'[x], y[0] == Zeros[0], 
    WhenEvent[y[x] == 0, Sow[{z -> x}]]}, 
   y, {x, -1, 40}]) // AbsoluteTiming

(* {0.302113,
    {{z -> 4.43216}, {z -> 7.68556}, {z -> 10.8744}, {z -> 14.0424},
     {z -> 17.2009}, {z -> 20.3543}, {z -> 23.5046}, {z -> 26.6528},
     {z -> 29.7997}, {z -> 32.9456}, {z -> 36.0907}, {z -> 39.2353}}} *)
Michael E2
  • 235,386
  • 17
  • 334
  • 747
  • Nice! Why do you use 1 for AccuracyGoal and PrecisionGoal? – Sjoerd C. de Vries Nov 14 '13 at 07:34
  • @SjoerdC.deVries Lowering AccuracyGoal and PrecisionGoal makes NDSolve faster, because the algorithm terminates when the goals are achieve. If you're is going to post-process with FindRoot, you use NDSolve only to approximate the roots close enough that FindRoot converges quickly. It's possible for errors to accumulate so that the estimates given by NDSolve miss a root, in which case I would increase them. – Michael E2 Nov 14 '13 at 12:33
  • Thank you, I think my answer has been answered sufficiently now. – Jeremy Upsal Nov 14 '13 at 16:54