I wanted to find the probability of my normally-distributed random variable being at least 15, so I set up this integral:
Integrate[PDF[NormalDistribution[14, 3.7], x], {x, 15, Infinity}]
Imagine my surprise when I got this result:
0.393476 - 1.75334*10^-15 I
Granted, the angle is miniscule. But why is Mathematica producing this result? This happens even if I type in the PDF manually:
0.107822 E^(-0.036523 (-14 + x)^2)
My TI in rectangular mode returns a result equal to the real component of what Mathematica produces. No complex component.
It doesn't make sense for a real-valued function to have complex area anyway. What's going on here? Whenever I see e's and i's in the same room I tend to blame Euler, but I'm having trouble figuring out what Mathematica is doing.
Using the "proper" Mathematica command for computing this probability returns a value that agrees with my calculator.
Probability[15 <= x, x \[Distributed] NormalDistribution[14, 3.7]]
I just want to know why Mathematica thinks the integral has complex area.

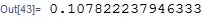


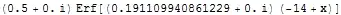
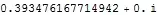
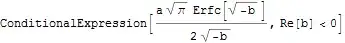
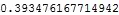
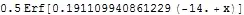

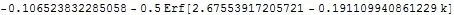
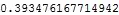




Integratecan do"interesting" things when one mixes approximate numbers with what is really a set of symbolic methods.NIntegrate, being more appropriate for numeric functionality, will not give this imaginary fuzz. – Daniel Lichtblau Nov 15 '13 at 17:12