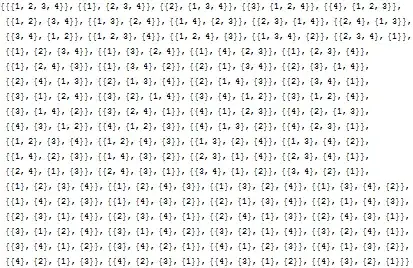Hope there is a solution besides the tedious generation of nested loops. (Trying to avoid reinventing the wheel.)
Here is an example with $N = 3$ objects. There are $13$ needed orderings (first {} means first place, second {} means second place, ...):
1. {a}, {b}, {c}
2. {a}, {c}, {b}
3. {a}, {b, c}
4. {b}, {a}, {c}
5. {b}, {c}, {a}
6. {b}, {a, c}
7. {c}, {a}, {b}
8. {c}, {b}, {a}
9. {c}, {a, b}
10. {a, b}, {c}
11. {a, c}, {b}
12. {b, c}, {a}
13. {a, b, c}
How can I get all such orderings for a given $N$?
UPD: I also wonder how to get same orderings in binary relations notation, i.e., considering orderings as sets of ordered pairs (also neglecting here such pairs as $(a,a)$, $(b,b)$, ... since they don't make further difference). I found out that this notation is much easier way to further operating with rankings in Mathematica. Here are the above $13$ orderings in new notation:
1. {(a,b), (a,c), (b,c)}
2. {(a,c), (a,b), (c,b)}
3. {(a,b), (a,c), (b,c) (c,b)}
4. {(b,a), (b,c), (a,c)}
5. {(b,c), (b,a), (c,a)}
6. {(b,a), (b,c), (a,c), (c,a)}
7. {(c,a), (c,b), (a,b)}
8. {(c,b), (c,a), (b,a)}
9. {(c,a), (c,b), (a,b), (b,a)}
10. {(a,b), (b,a), (a,c), (b,c)}
11. {(a,c), (c,a), (a,b), (c,b)}
12. {(b,c), (c,b), (b,a), (c,a)}
13. {(a,b), (b,a), (a,c), (c,a), (b,c), (c,b)}