Concatenation of lists in a Fibonacci-like pattern

Question

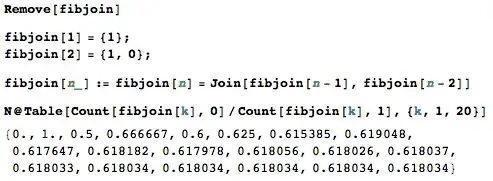
I am trying to create a List of elements that follow the general pattern:

$$X_{n+1} = X_n X_{n-1}$$

where the operation on the right hand side is concatenation, i.e., joining.

I want to achieve the following pattern:

$X_0 = \{1\}$
$X_1 = \{1,0\}$
$X_2 = X_1X_0 = \{1,0,1\}$
$X_3 = X_2X_1 = \{1,0,1,1,0\}$
$X_4 = X_3X_2 = \{1,0,1,1,0,1,0,1\}$
$X_5 = X_4X_3 = \{1,0,1,1,0,1,0,1,1,0,1,1,0\}$

This is much like a Fibonacci sum but is more like a Fibonacci joining. If you notice, the dimension of the $n^\text{th}$ set is the $n^\text{th}$ Fibonacci number.

I have gone along the lines of a Do loop but I don't know how to loop the current output with a previous output. My feeble attempts have bee thus far:

X0 = {1};X1 = {1, 0};t = Join[X0, X1];Do[Print[t];t = Join[t, t], {3}]

whose out put is

{1,1,0}
{1,1,0,1,1,0}
{1,1,0,1,1,0,1,1,0,1,1,0}

Now this is just joining the two sets three times. How do I join the set with a previous output one? Is there a tool to use that is easier/more efficient than the Do loop?

score 14 · Answer 1 · answered Nov 24 '13 at 14:09

It is so-called Rabbit sequence. One can notice that at each step

$$ 0 \to 1, \quad 1 \to 10. $$

The substitution $0\to1$ corresponds to young rabbits growing old, and $1\to10$ corresponds to old rabbits producing young rabbits.

fib[n_] := Nest[Flatten[# /. {0 -> {1}, 1 -> {1, 0}}] &, {1}, n]
fib[5]
(* {1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0} *)

It is not as efficient as Simon Woods's solution, but this alternative method in my opinion is also interesting.

Furthermore, the limiting sequence $1, 0, 1, 1, 0, 1, 0, \ldots$ is the binary representation of the rabbit constant

r = Sum[N[1/2^Floor[k*GoldenRatio], 120], {k, 0, 300}] - 1
(* 0.70980344286129... *)

RealDigits[r, 2][[1]]
(* {1, 0, 1, 1, 0, 1, 0, 1, 1, 0, ... } *)

You need a ternary computer to represent male and female rabbits :D — Dr. belisarius, Nov 24 '13 at 17:05

score 12 · Accepted Answer · answered Nov 24 '13 at 12:19

12

Why not just use a recursive definition like you would for a regular Fibonnaci function?

ClearAll[fibjoin]

fibjoin[0] = {1};
fibjoin[1] = {1, 0};

mem : fibjoin[n_] := mem = Join[fibjoin[n - 1], fibjoin[n - 2]]

fibjoin[5]
(* {1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0} *)

answered Nov 24 '13 at 12:19

Simon Woods

84,945
8
175
324

Thank you! What part does the function/expression "mem" play here? I am new to Mathematica and I have never seen this being used. I need to understand my code as well, not just be able to use it :). – user106492 Nov 24 '13 at 13:05
@user106492, it's for memoization - so that fibjoin remembers results it has previously found. Without it recursive functions like this are terribly inefficient. Have a look at this question for some discussion. – Simon Woods Nov 24 '13 at 13:20
4

Unfortunately fibjoin produces unpacked array. I propose to add Developer`ToPackedArray to {1} and {1,0}. It is ~2 times faster and uses ~4 times less memory. – ybeltukov Nov 24 '13 at 14:14
Cacheing + recursive pattern is always delicious in solving this problem. Just a quick note here: for large amount of recursion you may increase the limit by this link – yshk Nov 25 '13 at 05:16

Mr.Wizard · Answer 3 · 2013-11-24T15:52:08.823

Here is an iterative approach:

f1 = Flatten @ Nest[{#, #[[1]]} &, {1, 0}, # - 1] &;

f1 @ 5

{1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0}

I find this nice and clean, but it doesn't handle a zero argument, and it's not particularly efficient. Here is a variation to address both points:

f2 = First @ Nest[{Join @@ #, #[[1]]} &, Developer`ToPackedArray /@ {{1}, {0}}, #] &;

Array[fx, 6, 0] // Grid

$ \begin{array}{ccccccccccccc} 1 & & & & & & & & & & & & \\ 1 & 0 & & & & & & & & & & & \\ 1 & 0 & 1 & & & & & & & & & & \\ 1 & 0 & 1 & 1 & 0 & & & & & & & & \\ 1 & 0 & 1 & 1 & 0 & 1 & 0 & 1 & & & & & \\ 1 & 0 & 1 & 1 & 0 & 1 & 0 & 1 & 1 & 0 & 1 & 1 & 0 \end{array} $

score 2 · Answer 4 · answered Nov 24 '13 at 12:30

2

If you want a Do-based solution:

Block[{a = {1, 0}, b = {1}, n = 5},
 Do[
  {a, b} = {a~Join~b, a},
  {n - 1}]; 
 a]

will return the nth term, for n >= 1. (I'm feeling too lazy to package this into a function, but you can do that.)

answered Nov 24 '13 at 12:30

Aky

2,719
12
19

score 1 · Answer 5 · answered Nov 24 '13 at 14:38

1

Pluto[n_Integer] := 
 Block[{s1 = {1}, s2 = {1, 0},s3 = {}}, {Table[{s3 = {s2, s1} // Flatten, s1 = s2, 
     s2 = s3}, {n}]}; s3]

Call as Pluto[4]

{1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0}

answered Nov 24 '13 at 14:38

Pankaj Sejwal

2,063
14
23

yshk · Answer 6 · 2013-11-25T18:46:13.523

1

This number is amazing. When it comes to Fibonacci, we cannot get rid of golden ratio. Just compare the count of zeros and ones:

Remove[fibjoin]
fibjoin[1]={1};
fibjoin[2] = {1,0};
fibjoin[n_] :=  fibjoin[n] =  Join[fibjoin[n-1], fibjoin[n-2]]

N@Table[Count[fibjoin[k],0]/Count[fibjoin[k],1] , {k,1,20}]

godenratio

edited Nov 25 '13 at 18:46

answered Nov 25 '13 at 05:35

yshk

303
2
7

3

It would be better if you post code instead of the picture. Other users will be able to copy the code use it. – ybeltukov Nov 25 '13 at 12:49
1

Just updated. Thanks for reminding me. – yshk Nov 25 '13 at 18:46

ubpdqn · Answer 7 · 2013-11-25T22:19:44.500

0

I am very late to this but another (not very pretty) interative approach:

f[n_] := First@Nest[{#[[2]], Join[#[[2]], #[[1]]]} &, {{1}, {1, 0}}, n]

It handles f[0] and f[1] automatically...

edited Nov 25 '13 at 22:19

answered Nov 25 '13 at 12:02

ubpdqn

60,617
3
59
148

Concatenation of lists in a Fibonacci-like pattern

7 Answers7