Draw an arbitrary convex polyhedron without excess diagonals drawn

Question

I want to draw a set of convex polyhedrons whose vertices are defined by spherical coordinates on the surface of a unit sphere.

Currently I followed the advice from here: https://mathematica.stackexchange.com/a/21842/651 But it draws diagonals on any tetragonal face. Each face is composed of triangles. Is it possible to accomplish the same but without tetragonal faces diagonaled?

The current code:

Needs["TetGenLink`"]
mapping[{1,0,0}]={0,0,1}
mapping[{1,Pi,0}]={0,0,-1}
mapping:=CoordinateTransformData[{"Spherical"->"Cartesian"},"Mapping"]
verteces[n_]:=Flatten[Table [{1,Pi k/n, i 2Pi/Binomial[n,k]},{k,0,n},{i,0,Binomial[n,k]-1}],1]
Convex[n_]:=TetGenConvexHull[mapping/@ verteces[n]]
pts[n_]:=First[Convex[n]]
surface[n_] :=Last[Convex[n]]
b:=5
Graphics3D[{Yellow,Opacity[.9],GraphicsComplex[pts[b],Polygon[surface[b]]], Black, Line[{{0,0,-1.1},{0,0,1.1}}]}]

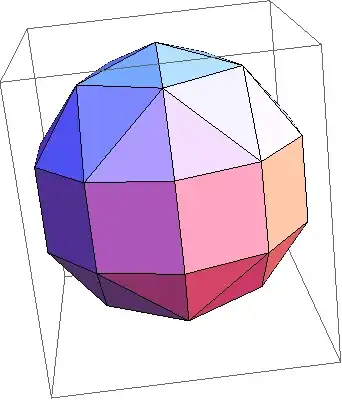
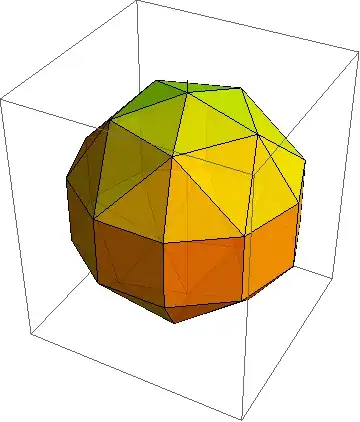
You can do this: take the triangle list surface[b]. Find the edges. Each edge has two neighbouring triangles. For each edge, if those two triangles are parallel (the dot product of their normals is 1 to a certain precision), merge them into a tetragon. Can you try to implement this? — Szabolcs, Nov 26 '13 at 22:31
Quick fix would be to skip edges with: GraphicsComplex[pts[b], {EdgeForm[None], Polygon[surface[b]]}] — Kuba, Nov 26 '13 at 22:32
Or what Kuba said, that's even better: loop through edges, and do not render those that have parallel adjacent polygons. — Szabolcs, Nov 26 '13 at 22:33
@Kuba I already tried it. Without edges the picture is uncomprehensible where there are many faces. — Anixx, Nov 26 '13 at 22:40

Dr. belisarius · Accepted Answer · 2013-11-27T04:05:18.823

8

<< ComputationalGeometry`
ComputationalGeometry`Methods`ConvexHull3D[mapping /@ verteces[5], 
                                           Axes -> None, Graphics`Mesh`FlatFaces -> False]

Mathematica graphics

Mapping over n (well, with a trick because it fails with more than three calculations in a row):

Mathematica graphics

Edit

merging with your code:

<< ComputationalGeometry`
mapping[{1, 0, 0}] = {0, 0, 1}
mapping[{1, Pi, 0}] = {0, 0, -1}
mapping := CoordinateTransformData[{"Spherical" -> "Cartesian"}, "Mapping"]
verteces[n_] := Flatten[Table[{1, Pi k/n, i 2 Pi/Binomial[n,k]}, {k,0,n}, {i, 0,Binomial[n,k]-1}], 1]

Graphics3D[{Yellow, Opacity[.9], 
           Sequence @@ ComputationalGeometry`Methods`ConvexHull3D[mapping /@ verteces[5], 
           Axes -> None, Graphics`Mesh`FlatFaces -> False],Black,Line[{{0, 0, -1.1}, {0, 0, 1.1}}]}]

Mathematica graphics

edited Nov 27 '13 at 04:05

answered Nov 26 '13 at 23:17

Dr. belisarius

115,881
13
203
453

Magic again! +1 – PlatoManiac Nov 26 '13 at 23:27
While your result is great, I do not know how to implement it. Where should I put this function? – Anixx Nov 26 '13 at 23:28
@Anixx It's using your mapping and verteces :) just run it after your code – Dr. belisarius Nov 26 '13 at 23:32
How to use the result of this function? I tried to insert it in Graphics3D but it does not work – Anixx Nov 26 '13 at 23:33
Oh, I got it how. – Anixx Nov 26 '13 at 23:36
So what hach you did to make a table? – Anixx Nov 26 '13 at 23:38
I did the following: Hull[n_]:=Cases[ComputationalGeometryMethodsConvexHull3D[mapping/@verteces[n],Axes->None,GraphicsMeshFlatFaces->False],_GraphicsComplex,Infinity] and it works but does not work if I want to make a table of such polyhedra – Anixx Nov 26 '13 at 23:41
@Anixx ComputationalGeometryMethodsConvexHull3D[mapping /@ verteces[#], Axes -> None, GraphicsMeshFlatFaces -> False] & /@ Range[5, 7] – Dr. belisarius Nov 26 '13 at 23:43
@belisarius without range the table draws 3 polyhedra, with this addition only one – Anixx Nov 26 '13 at 23:48
@belisarius I see 3 graphics – Anixx Nov 26 '13 at 23:51
With Table, the fourth graphic gives an error – Anixx Nov 26 '13 at 23:52
Range[5,8] also gives an error – Anixx Nov 26 '13 at 23:53
Okay, this is another question, I think. – Anixx Nov 26 '13 at 23:56
@Anixx Re-read my answer. I wrote Mapping over n (well, with a trick because it fails with more than three calculations in a row): – Dr. belisarius Nov 26 '13 at 23:56
@belisarius I see, that's why it is an unrelated topic and deserves another question. – Anixx Nov 26 '13 at 23:57
Seems does not work in Mathematica 10. – Anixx Nov 09 '14 at 01:10
@Anixx No way to test it here. Still on v9 – Dr. belisarius Nov 09 '14 at 05:00
@Anixx Since Version 10, all methods of the ComputationalGeometry package are included in the core Mathematica system. See e.g. ConvexHullMesh etc. – András Aszódi Apr 26 '17 at 09:23

PlatoManiac · Answer 2 · 2013-11-27T03:22:42.730

Here is another solution using coplanar triangles idea. Given six vertices of two triangles that share an adjacent edge, we use EigenValues to estimate the mean-square orthogonal distance of the points from the best fitting plane. In case it turns out to be close to zero we can assume the two triangles under consideration are coplanar with in some tolerance. You will find more details here. Once we know this for any two neighboring triangle in the TetGen mesh we can form a Quad by joining them.

trigToedge[list_] := Partition[list, 2, 1, 1]; 
Quad[current_, {pt_, tri_}] := 
 Block[{trigtopt, threeTigs, connectedTrigs, dist, mat, test,coplanar, edges},
  trigtopt[list_] := Extract[pt, Transpose@{list}];
  threeTigs = Select[tri, Length@Intersection[#, current] == 2 &];
  connectedTrigs = (trigtopt[#] & /@ threeTigs);
  dist = (
      mat = (# - Mean@#) & /@ (Transpose@(trigtopt[current]~Join~#));
      Min@Chop@Eigenvalues[(mat . Transpose@mat)/6]
      ) & /@ connectedTrigs;
  test = Position[dist, 0];
  {coplanar} = If[test != {}, Extract[threeTigs, test], {0}];
  If[Length@coplanar == 3, 
   edges = Cases[
     Tally[Join @@ (trigToedge /@ {current, coplanar}),
        (#1 == Reverse[#2] &)], {a_, 1} -> a];
   DeleteDuplicates@Flatten@Sort[edges, First@#2 == Last@#1 &], 
   current]
  ];

Testing:

b = 9;
tri = surface[b];
pt = pts[b];
poly = Quad[#, {pt, tri}] & /@ tri;
Graphics3D[{GraphicsComplex[pt, Polygon[poly]], Black}, Boxed -> False, ImageSize -> 350]

enter image description here

As expected we have now the quads whenever they occur for odd b values. The current implementation is not optimal for very large meshes but the underlying mathematics is interesting!

Draw an arbitrary convex polyhedron without excess diagonals drawn

2 Answers2

Linked