The functions Re and Im (just as Conjugate) don't satisfy the Cauchy-Riemann differential equations and are therefore not analytic. That means their derivative is not uniquely defined in the complex plane. That's the reason why Re' and Im' can't be simplified.
Therefore, we have to be more specific about how we want the limit to be done that corresponds to the desired derivative. The cleanest way of doing that is this simple replacement for the derivative:
Limit[(Gamma[I (x + ε)] - Gamma[I x])/ε, ε -> 0]
$i \Gamma (i x) \psi ^{(0)}(i x)$
Now I'll try to apply this to the real part instead:
Assuming[Element[x, Reals], Limit[(Re[Gamma[I (x + ε)]] - Re[Gamma[I x]])/ε, ε -> 0]]
$-\Im(\psi ^{(0)}(i x)) \Re(\Gamma (i x))-\Im(\Gamma (i x))
\Re(\psi ^{(0)}(i x))$
So we don't get any of the pesky Re' here. For those who don't like the $\LaTeX$ format, here is the real output:
-Im[PolyGamma[0, I x]] Re[Gamma[I x]] - Im[Gamma[I x]] Re[PolyGamma[0, I x]]
Edit: generalization
Motivated by the discussion of Heike's answer, I wrote a definition of a directional derivative in an arbitrary direction in the complex plane. I did this to show that such a definition can be made without in any way modifying SystemOptions (see in particular "More Information").
dirDeriv[f_, var_, angle_: 0] := Module[{g, x},
g = f /. var -> x;
Assuming[x ∈ Reals,
D[g, x] /. (h_'[p_] :> h'[p]/D[p, x]) /. (h_'[p_] :>
Limit[(h[p /. x -> x + ε Exp[I angle]] -
h[p])/ε/Exp[I angle], ε -> 0]) /.
x -> var
]
]
The first argument is the function to be differentiated, the second argument is the name of the independent variable, which will be treated as a real number. The third (optional) argument is the phase angle of the line in the complex plane along which the limit for the derivative is taken. By default this angle is zero corresponding to the real axis (the result depends on the angle only if the first argument is non-analytic).
Here is how to apply this function as a replacement for the standard derivative:
dirDeriv[Re[Gamma[I x]], x]
$-\Im(\psi ^{(0)}(i x)) \Re(\Gamma (i x))-\Im(\Gamma (i x))
\Re(\psi ^{(0)}(i x))$
A simpler example is
dirDeriv[Re[Exp[I x^2]], x]
$-2 x \sin \left(x^2\right)$
The function works by doing the standard derivative and then looking for any occurrences of Re', Im' and others (in fact, anything looking like h_'[p_]). These patterns are then replaced by first undoing the chain rule that Mathematica automatically applies (that's the division by D[p, x]), and then calculating the directional derivative as a limit analogous to the example above.
With this function one can easily explore the direction dependence of the derivative for non-analytic functions. For example,
Table[dirDeriv[Re[x], x, angle], {angle, 0, Pi, Pi/4}]
{1, 1/2 - I/2, 0, 1/2 + I/2, 1}
Edit 2: numerical functions
The above discussion concerns symbolic directional derivatives of possibly non-analytic functions. The situation is in some ways much simpler if the goal is to do numerical differentiation, i.e., calculate the derivative of a function f[x] which is numeric when the argument x is numeric.
For that case, one can go straight to the numerical approach by doing this:
Needs["NumericalCalculus`"];
ND[Re[Gamma[I x]], x, 1]
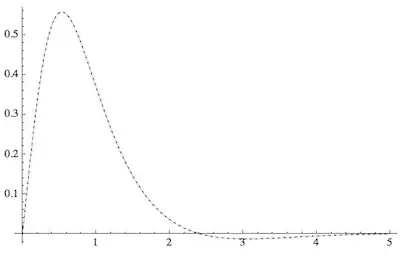
With the numerical derivative ND, you can for example make plots directly. Here is a comparison of the symbolic result with the numerical one:
Plot[{
-Im[PolyGamma[0, I x0]] Re[Gamma[I x0]] -
Im[Gamma[I x0]] Re[PolyGamma[0, I x0]],
ND[Re[Gamma[I x]], x, x0]},
{x0, 0, 5}, PlotStyle -> {Thin, Dotted}]

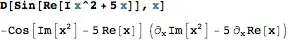
xis a real variable, thenD[Re[f[x]],x]isRe[f'[x]],D[Im[f[x]],x]isIm[f'[x]]andD[Arg[f[x]],x]isIm[f'[x]/f[x]]. I don't think this can be handled by giving a value toRe'[f[x]],Im'[f[x]]andArg'[f[x]](but if I'm wrong and it can, that would allow to fix up the expression using simple replacement rules). – celtschk Apr 01 '12 at 19:11Re,ImandArg, I want to take the derivative of functions of real variables containing them. And those derivatives are defined (as long as the functions are otherwise well-behaved). – celtschk Apr 01 '12 at 19:58D[Im@f@x,x] = Im´[f[x]] f´[x]
– Searke Apr 01 '12 at 20:20Im'as acting on functions instead of values, withIm'[f[x]] = Im[f'[x]]/f'[x]. I'll have to think about that idea. – celtschk Apr 01 '12 at 21:01