How to find the vertices of a regular tetrahedron? a dodecahedron?

Question

My question is: how to find the coordinates of the vertices of regular tetrahedron and dodecahedron? I tried to find the coordinates of the vertices of a regular tetrahedron as the solutions of a certain polynomial system in $8$ variables, notating the vertices of a tetrahedron $S(0,0,1)$, $A(0,yA,zA)$, $B(xB,yB,zB)$, and $C(xC,yC,zC)$:

Reduce[
yA^2 + zA^2 == 1 &&
xB^2 + yB^2 + zB^2 == 1 && 
xC^2 + yC^2 + zC^2 == 1 && 
yA^2 + (zA - 1)^2 == xB^2 + yB^2 + (zB - 1)^2 && 
yA^2 + (zA - 1)^2 == xC^2 + yC^2 + (zC - 1)^2 && 
xB^2 + (yB - yA)^2 + (zB - zA)^2 ==
                 xC^2 + (yC - yA)^2 + (zC - zA)^2 && 
xB^2 + (yB - yA)^2 + (zB - zA)^2 ==
                 (xC - xB)^2 + (yC -yB)^2 + (zC - zB)^2 && 
xB^2 + (yB - yA)^2 + (zB - zA)^2 == 
                 yA^2 + (zA - 1)^2,
        {xB, xC, yA, yB, yC, zA, zB, zC}, Reals]

However, that code is spinning for hours without any output. A new idea is required.

P.S. 12.12.13. The answer done with Maple can be seen at http://mapleprimes.com/questions/200438-Around-Plato-And-Kepler-Again. Because nothing but trigonometry is used, I am pretty sure all that is possible in Mathematica.

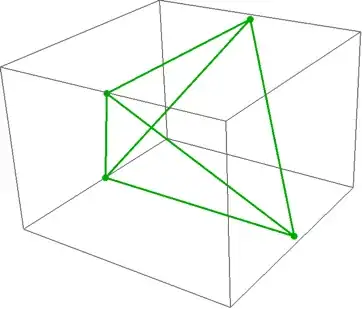
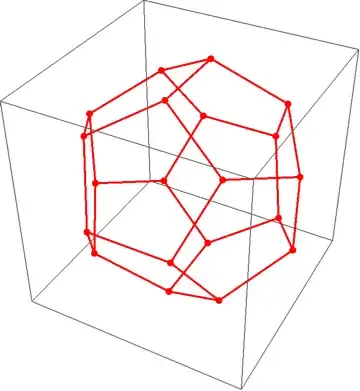
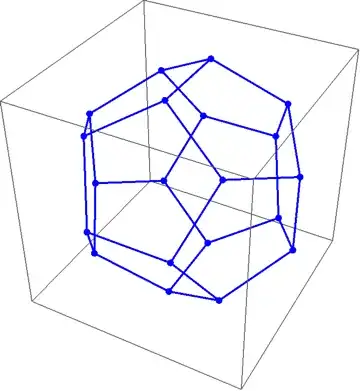
You can use PolyhedronData unless you are genuinely interested in calculating the vertices. — C. E., Dec 10 '13 at 15:25
As far as I understand it, these coordinates are implemented in PolyhedronData. The question is how to calculate the ones exactly, not numerically, in Mathematica. — user64494, Dec 10 '13 at 15:36
I don't understand you saying "As far as I understand it," in the comment above ... it's your question! Or is it homework? — Dr. belisarius, Dec 10 '13 at 16:23
@ belisarius: This is my question, not a homework. I am professor for ages. — user64494, Dec 10 '13 at 16:31
What are the constraints on this tetrahedron? That all vertex distances to roigin be 1? If so, is there a reason not to place the last three points in the x-y plane? Doing so should simplify the equations, especially as one can be placed, say, on the x axis. — Daniel Lichtblau, Dec 10 '13 at 16:52
@ Daniel Lichtblau: It should be a regular tetrahedron/dodecahedron. If the three vertices belong to the xOy plane, that does not simplify matter as we don't know the location of the fourth one. — user64494, Dec 10 '13 at 17:43
You can extract the exact coordinates of the vertices a regular tetrahedron (for instance) using PolyhedronData["Tetrahedron"] // Cases[#, GraphicsComplex[x_, _] :> x] &. — Stephen Luttrell, Dec 10 '13 at 19:20
@ Stephen Luttrell: Of course,the exact coordinates of the vertices a regular tetrahedron/dodecahedron are known in Mathematica. The problem is to derive those, not to extract those. — user64494, Dec 10 '13 at 19:37
Four alternate vertices of a cube are the vertices of a regular tetrahedron. If they are rotated about a certain axis by 1/5, 2/5, etc of a turn, you get the vertices of a regular dodecahedron. Would that be any help? — Michael E2, Dec 10 '13 at 19:40
Place three vertices in the x-y plane. You know they are on an equilateral triangle. Place one on the x axis at {1,0,0}. Assume the centroid of this triangle is the origin. Then you know the fourth vertex is above it, hence has vertex {0,0,z}. The second and third, by symmetry, are at {x,y,0} and {x,-y,0}. The equations that result will be much easier to handle. Also it's not hard to find x and y without a computer, and from there to find z. — Daniel Lichtblau, Dec 10 '13 at 19:52
@ Daniel Kichtblau: Your suggestion is rather by hand than with Mathematica. What do you suggest for a regular dodecadron? — user64494, Dec 10 '13 at 20:05
My suggestion is not really by hand. It's just a matter of choosing sensible coordinates in order to do a computation. You can remove the "by symmetry" knowledge and probably still get a viable computation. — Daniel Lichtblau, Dec 12 '13 at 16:06

score 6 · Accepted Answer · edited Apr 13 '17 at 12:56

Invariant theory construction

We can use Klein's invariants ($\Phi'$ on page 55, $H$ on page 61, Lectures on the Icosahedron) and project the complex roots onto the Riemann sphere, borrowing ubpdqn's projection code:

tetraPoly = -z1^4 - 2 Sqrt[3] z1^2 z2^2 + z2^4;
dodecaPoly = z1^20 + z2^20 - 228 (z1^15 z2^5 - z1^5 z2^15) + 494 z1^10 z2^10;

 (* project onto the Riemann sphere *)
sph[z_?NumericQ] := 
  Module[{den}, den = 1 + Re[z]^2 + Im[z]^2; {2 Re[z]/den, 2 Im[z]/den, (den - 2)/den}];

vTetra2 = sph[z1] /. Solve[(tetraPoly /. z2 -> 1) == 0, z1];

vDodeca2 = sph[z1] /. Solve[(dodecaPoly /. z2 -> 1) == 0, z1];
nf = Nearest[N@vDodeca2 -> Automatic];
edgeIndices2 = 
  Flatten[Cases[nf[vDodeca2[[#]], 4], n_ /; n > # :> {#, n}] & /@ Range[1, 19], 1];

Tetrahedron:

Graphics3D[GraphicsComplex[vTetra2,
  {Darker@Green, Thick, PointSize[Large],
   Point[Range@4],
   Line[Subsets[Range@4, {2}]]
   }]
 ]

tetrahedron

Dodecahedron:

Graphics3D[GraphicsComplex[vDodeca2,
  {Darker@Green, Thick, PointSize[Large],
   Point[Range@20],
   Line[edgeIndices2]
   }]
 ]

dodecahedron

This approach is very interesting. Could you explain the interplay between http://en.wikipedia.org/wiki/J-invariant and a dodecahedron in detail? — user64494, Dec 14 '13 at 08:08
@user64494 Thanks. I added references. It's based on rather famous work of Felix Klein on solving 5th-degree polynomial equations. — Michael E2, Dec 14 '13 at 13:34
@ Michael E2: This is it. Your answer is complete in both Mathematical and mathematical senses. — user64494, Dec 14 '13 at 14:36

Michael E2 · Answer 2 · 2013-12-12T19:16:45.900

A geometric construction

The alternate vertices of a cube are the vertices of a regular tetrahedron. Rotate these about an appropriate axis (for an explanation of the mathematics, see, for example, Euclid, Prop. XIII.17 or this demonstration) five times through a 1/5 turn and you get the vertices of a regular dodecahedron. In the construction below, one can choose any three mutually perpendicular vectors of the same length for e1, e2, e3 to define the edges of the cube. The cube will be centered at the origin with edges of twice the length of e1. Different choices yield different orientations and sizes.

{e1, e2, e3} = IdentityMatrix[3];
n0 = e1 + GoldenRatio e3; (* axis of rotation *)
vTetra = {{1, 1, 1}, {-1, -1, 1}, {1, -1, -1}, {-1, 1, -1}}.{e1, e2, e3};
vDodeca = Flatten[NestList[#.RotationMatrix[2 Pi/5, n0] &, vTetra, 4], 1];
nf = Nearest[N@vDodeca -> Automatic];
edgeIndices = 
  Flatten[Cases[nf[vDodeca[[#]], 4], n_ /; n > # :> {#, n}] & /@ Range[1, 19], 1];

Tetrahedron

vTetra
(* {{1, 1, 1}, {-1, -1, 1}, {1, -1, -1}, {-1, 1, -1}} *)

Graphics3D[GraphicsComplex[vTetra,
  {Red, Thick, PointSize[Large],
   Point[Range@4],
   Line[Subsets[Range@4, {2}]]
   }]
 ]

Mathematica graphics

Dodecahedron

vDodeca /. GoldenRatio -> (1 + Sqrt[5])/2 // Simplify

(* {{1, 1, 1}, {-1, -1, 1}, {1, -1, -1}, {-1, 1, -1},
    {1/2 (1 + Sqrt[5]), 0, 1/2 (-1 + Sqrt[5])}, {-1, 1, 1},
    {1/2 (1 - Sqrt[5]), 1/2 (-1 - Sqrt[5]), 0}, {0, 1/2 (-1 + Sqrt[5]), 1/2 (-1 - Sqrt[5])},
    {1, -1, 1}, {1/2 (-1 + Sqrt[5]), 1/2 (1 + Sqrt[5]), 0},
    {1/2 (-1 - Sqrt[5]), 0,  1/2 (-1 + Sqrt[5])}, {0, 1/2 (1 - Sqrt[5]), 1/2 (-1 - Sqrt[5])},
    {0, 1/2 (1 - Sqrt[5]), 1/2 (1 + Sqrt[5])}, {1/2 (1 + Sqrt[5]), 0, 1/2 (1 - Sqrt[5])},
    {1/2 (1 - Sqrt[5]), 1/2 (1 + Sqrt[5]), 0}, {-1, -1, -1},
    {0, 1/2 (-1 + Sqrt[5]), 1/2 (1 + Sqrt[5])}, {1/2 (-1 + Sqrt[5]), 1/2 (-1 - Sqrt[5]), 0},
    {1, 1, -1}, {1/2 (-1 - Sqrt[5]), 0, 1/2 (1 - Sqrt[5])}} *)

Graphics3D[GraphicsComplex[vDodeca,
  {Red, Thick, PointSize[Large],
   Point[Range@20],
   Line[edgeIndices]
   }]
 ]

Mathematica graphics

@ Michael E2 : You wrote " Rotate these about an appropriate axis (see for example, Euclid, Prop. XIII.17 or this demonstration) five times through a 1/5 turn and you get the vertices of a regular dodecahedron". Could you elaborate that place in detail? — user64494, Dec 12 '13 at 16:01
@user64494 From Euclid's proof it follows that e1 + GoldenRatio e3, where e1, e2, e3 are mutually orthonormal vectors, is normal to a face of the dodecahedron. It also follows that when a cube centered at the origin with edges parallel to one of e1, e2,e3is rotated about this normal by a2 Pi k / 5, the vertices of the cube land on vertices of the dodecahedron constructed in XIII.17. The alternate vertices of the cube land on all the vertices of the dodecahedron exactly once whenkranges from0to4`. The rest of the explanation can be found in Euclid. — Michael E2, Dec 12 '13 at 19:00
@ Michael E2 : Thank you for the explanation. However, all that is done rather by hand than with Mathematica. — user64494, Dec 12 '13 at 19:51
@user64494 I don't understand. The dodecahedron was done by Mathematica and certainly not by hand (not by mine). And a cube is so simple, why cavil? It seems to me that the approach in the question is done by hand as well -- who made up and entered the equations? It seems a certain amount of "by hand" is necessary. Please explain clearly what you want. — Michael E2, Dec 12 '13 at 23:47

george2079 · Answer 3 · 2013-12-12T20:43:05.980

Actually It turns out mathematica can nicely directly solve the posed system of quadratics...

This should be equivalent to the formulation posed in the question:

$Assumptions = {Element[x[i_, j_], Reals]}
pts = Table[ x[i, j] , {i, 4}, {j, 3}] 
pts[[1]] = {0, 0, 1}
pts[[2, 1]] = 0
soln = Solve[Simplify[(Norm[#]^2 == 1 & /@ pts)~Append~
    (Equal @@ 
      Simplify[
         Norm[pts[[#[[1]]]] - pts[[#[[2]]]]]^2 & /@  
         Subsets[Range[4], {2}]])], Cases[Flatten@pts, x[_, _]]];

Last@soln  (*just by observation the last solution is real *)


(*
   {x[2, 2] -> -((2 Sqrt[2])/3), x[2, 3] -> -(1/3), x[3, 1] -> Sqrt[2/3],
    x[3, 2] -> Sqrt[2]/3, x[3, 3] -> -(1/3), x[4, 1] -> -Sqrt[(2/3)], 
    x[4, 2] -> Sqrt[2]/3, x[4, 3] -> -(1/3)}
*)

Graphics3D[
  Line[{pts[[#[[1]]]], pts[[#[[2]]]]}] & /@ Subsets[Range[4], {2}] /. 
  Last@soln, Boxed -> False]

I note that If I specify the Reals domain to solve it does not immediately return a solution, but by leaving out the domain it quickly returns 4 complex results and 4 real..

This works the same with Reduce noting the system of equations actually has 4 (I think) real solutions by symmetry (the tet can be upsidedown / mirrored..). Reduce returns a somewhat messy expression encompassing all the possibilities.

EDIT:

Just noticed the posed system admits the degenerate solution of all coincident points. This adds one more equation to exclude the degenerate case.

$Assumptions = {Element[x[i_, j_], Reals]};
n = 4;
pts = Table[ x[i, j] , {i, n}, {j, 3}] ;
pts[[1]] = {0, 0, 1};
pts[[2, 1]] = 0;
soln = Solve[Simplify[(Norm[#]^2 == 1 & /@ pts)~Append~
   (Equal @@ 
       Simplify[
           Norm[pts[[#[[1]]]] - pts[[#[[2]]]]]^2 & /@  
                Subsets[Range[n], {2}]])~Append~(pts[[2]] != pts[[1]])], 
                             Cases[Flatten@pts, x[_, _]]]

This should pull out the real solutions:

soln = Select[ soln  ,   Length[Union@Flatten[Simplify[Im[pts] /. #]]] == 1 &]

Unfortuately it only seems to work for n=4, not for 6,8,12 or 20..

Edit 2 -- well duh on me..the equations specify all points equidistant from each other, which is only the case for the tetrahedron. I'm not sure how to even pose the problem for a dodecahedron (That is as a sysem of equations w/o some other knowledge of the solution) Would it be cheating to use PolyhedronData["Dodecahedron", "EdgeIndices"] ?

@ george2079 : It is nice. How about a regular dodecahedron? — user64494, Dec 12 '13 at 17:09

Michael E2 · Answer 4 · 2013-12-15T00:41:54.370

Reflection group approach

Yet another approach in which Mathematica does most of the work. The starting point is to observe that if a face of a dodecahedron is subdivided into ten congruent right triangles, the group of symmetries of a dodecahedron is generated by reflections in planes that form a spherical triangle of angles $\pi/2$, $\pi/3$, and $\pi/5$ (triangle group (2, 3, 5)). The vertices of the dodecahedron are the orbit of the vertex v0 of the triangle where the angle is $\pi/3$. One starts with two planes at right angles to each other, and Mathematica solves for the third plane of reflection so that, given it is constructed so that it is inclined at an angle of $\pi/3$ to one initial plane, the plane of reflection is inclined at an angle of $\pi/5$ to the other initial plane.

refl[1] = ReflectionTransform[{1, 0, 0}];
refl[2] = ReflectionTransform[{0, 0, 1}];
refl[3] = 
  ReflectionTransform[{Sin[Pi/3] Cos[theta], Sin[Pi/3] Sin[theta], Cos[Pi/3]} /. 
    Last @ Quiet @
      Solve[VectorAngle[{1, 0, 0}, {Sin[Pi/3] Cos[theta], 
          Sin[Pi/3] Sin[theta], Cos[Pi/3]}] == Pi/5, theta]];
 (* basic rotational symmetries *)
rot[2] = Composition[refl[1], refl[2]];
rot[3] = Composition[refl[2], refl[3]];
rot[5] = Composition[refl[1], refl[3]];
 (* a convenient symmetry *)
rot[0] = Composition[rot[3], rot[5]];

 (* initial vertex *)
v0 = {Sin[Pi/2] Cos[theta - Pi/2], Sin[Pi/2] Sin[theta - Pi/2], Cos[Pi/2]} /. 
   Last @ Quiet @
     Solve[VectorAngle[{1, 0, 0}, {Sin[Pi/3] Cos[theta], 
         Sin[Pi/3] Sin[theta], Cos[Pi/3]}] == Pi/5, theta];
 (* 20 symmetries for transforming the initial vertex *)
rotDodeca = 
  NestList[Simplify @ Composition[rot[5], #] &, #, 4] & /@ 
    Simplify @ FoldList[Dot, 
      TransformationFunction@IdentityMatrix[4], {rot[0], rot[5], rot[0]}] // Flatten;

vDodeca3 = #[v0] & /@ rotDodeca; (* 20 vertices *)
nf = Nearest[N@vDodeca3 -> Automatic];
edgeIndices3 =  (* edges *)
  Flatten[Cases[nf[vDodeca3[[#]], 4], n_ /; n > # :> {#, n}] & /@ Range[1, 19], 1];

Dodecahedron:

Graphics3D[GraphicsComplex[vDodeca3,
  {Blue, Thick, PointSize[Large],
   Point[Range@20],
   Line[edgeIndices3]
   }]
 ]

Mathematica graphics

[Coordinates, which may vary with orientation, and tetrahedron omitted.]

Could you explain it in details? A good code is an explained one. — user64494, Dec 14 '13 at 08:10
@user64494 Thanks, again. I added a brief description and a link. I'm afraid I have rather a lot of grading to get through in the next few days. An extensive treatment of this subject is Coxeter, Regular Polytopes. — Michael E2, Dec 14 '13 at 13:37

A.G. · Answer 5 · 2013-12-12T18:45:15.320

Here is something that seems to work for the tetrahedron. I expect the dodecahedron would work the same way with more code-typing or a list trick (anyone knows how to do that?).

p1 := {x1, y1, z1};
p2 := {x2, y2, z2};
p3 := {x3, y3, z3};
p4 := {x4, y4, z4};
Solve[
    EuclideanDistance[p1, p2] == 1 &&
     EuclideanDistance[p1, p3] == 1 &&
     EuclideanDistance[p1, p4] == 1 &&
     EuclideanDistance[p2, p3] == 1 &&
     EuclideanDistance[p2, p4] == 1 &&
     EuclideanDistance[p3, p4] == 1 &&
     x1 == 0 && y1 == 0 && z1 == 0 &&
     x2 == 0 && y2 == 0 && z2 == 1 &&
     x3 == 0,
    {x1, y1, z1, x2, y2, z2, x3, y3, z3, x4, y4, z4}, Reals] // Last;
tetra = Partition[{x1, y1, z1, x2, y2, z2, x3, y3, z3, x4, y4, 
    z4} /. %, 3]

Output :

{{0, 0, 0}, {0, 0, 1}, {0, Sqrt[3]/2, 1/2}, {Sqrt[2/3], 1/(2 Sqrt[3]),
   1/2}}

score 0 · Answer 6 · answered Dec 10 '13 at 16:37

0

LinearProgramming[#,
{{1,1,1},{1,0,0},{0,1,0},{0,0,1}},
{{1,-1},{1,-1},{1,-1},{1,-1}},{0,0,0}]&/@{{-1,0,0},{0,-1,0},{0,0,-1},{1,1,1}}

As you want exact output, and not numeric output, you could use LinearProgramming. This function returns rational output for rational input. You just need the parametrization of the faces/facets that define your tetrahedron and the correct objective functions, one per node. You could now do the same for your dodecahedron example, or any polytope, for that matter -- including regular tetrahedra, simplices, and platonic solids or whatever else.

answered Dec 10 '13 at 16:37

Andreas Lauschke

4,009
22
20

Thank you for the interest to the question. Is this a right tetrahedron? How about a right dodecahedron? – user64494 Dec 10 '13 at 16:42
@ Andreas Lauschke: You wrote:"You just need the parametrization of the faces/facets that define your tetrahedron and the correct objective functions". This is a difficulty. – user64494 Dec 10 '13 at 16:50
@user64494:, yes that is indeed a difficulty. I never said it was easy, I wanted to show a very generic method that computes the coordinates of the nodes of polytopes, returning exact numbers (rationals). You could automate this, generate the equations/inequalities and rhs and objective functions from PolyhedronData, but a) this also wouldn't be very easy and b) why compute them if you can look them up directly? But, computing them was your requirement. – Andreas Lauschke Dec 10 '13 at 19:17
@ Andreas Lauschke: You have suggested a good idea to apply LinearProgramming.I treat the question under consideration as a touchstone. It is of serious interest how to solve problems of computational geometry with Mathematica. – user64494 Dec 10 '13 at 19:44

How to find the vertices of a regular tetrahedron? a dodecahedron?

6 Answers6

Linked