Numerical instability in cosh and sinh - integral functions

Question

I'm trying to calculate the function:

CoshIntegral[x] Sinh[x] - Cosh[x] SinhIntegral[x]

Unfortunately Mathematica seems to hit a point (x~20) and things become unstable (see plot below), there shouldn't be any infinities in the area, so I am rather confused as to what is going on!

plot of above function

Does anyone know why this is happening and how to fix it?

score 12 · Accepted Answer · answered Dec 13 '13 at 12:33

12

You are calculating the small difference between numbers which are getting quite large and the default WorkingPrecision of Plot (which is MachinePrecision, usually about 16) is just not high enough.

So simply increase the WorkingPrecision of Plot, e.g.

Plot[CoshIntegral[x] Sinh[x] - Cosh[x] SinhIntegral[x], {x, 0, 40}, 
 WorkingPrecision -> 40, PlotRange -> All]

answered Dec 13 '13 at 12:33

MikeLimaOscar

3,456
17
29

Perfect! Thanks for your help. – jake Dec 13 '13 at 12:37

tchronis · Answer 2 · 2013-12-13T12:32:34.247

8

I verified this behavior. I tried to increase $MaxExtraPrecision but I didn't get any improvement.

A solution is to increase WorkingPrecision in Plot:

Plot[CoshIntegral[x] Sinh[x] - Cosh[x] SinhIntegral[x], {x, 0, 30}, 
 WorkingPrecision -> 50, PlotRange -> {{0, 30}, {-1, 1}}]

enter image description here

At last I created Cosh and Sinh integrals below with increased WorkingPrecision inside NIntegrate.

chi[z_] := N[EulerGamma + Log[z] + 
             NIntegrate[(Cosh[t] - 1)/t, {t, 0, z}, WorkingPrecision -> 50], 50]

shi[z_] := NIntegrate[Sinh[t]/t, {t, 0, z}, WorkingPrecision -> 50]

Then we can define res[x] as:

res[x_] := N[chi[x] Sinh[x] - shi[x] Cosh[x],50]

And Plot it:

Plot[res[x], {x, 0, 30}, 
 WorkingPrecision -> 50, PlotRange -> {{0, 30}, {-1, 1}}]]

It is a little bit slow but it works.

To check special values you can also use CoshIntegral Evaluation to verify the correctness for chi function above.

edited Dec 13 '13 at 12:32

answered Dec 13 '13 at 11:20

tchronis

2,445
1
14
26

Thanks for the comment, unfortunately when I tried using the above method I still had the wacky behaviour. I think the Logarithm should be a natural log rather than base 10, and the integral should go to 0 as x->infty – jake Dec 13 '13 at 11:36
@jake I searched on http://functions.wolfram.com/GammaBetaErf/CoshIntegral/ and it seems that log has base 10. Also there you can download a PDF file (after completing a small form) with all information about the function. What version of Mathematica are you using ? – tchronis Dec 13 '13 at 11:55
I'm using mathematica 9. Thanks for that I will have a flick through. I was under the impression though, that the function Log[] in mathematica was by default a natural logarithm? – jake Dec 13 '13 at 12:04
@Jake yes you are right. I got confused - it is the natural logarithm. And for this change I get very strange results... I will update shortly. – tchronis Dec 13 '13 at 12:11
@tchronis You updated your answer at the same time I posted mine! – MikeLimaOscar Dec 13 '13 at 12:34
@MikeLimaOscar yes you were seconds faster than me! :-) – tchronis Dec 13 '13 at 12:38

score 5 · Answer 3 · answered Dec 13 '13 at 16:38

An alternative to setting the input precision is to ask for enough output accuracy. The main idea is to set the precision of the input to Infinity and use N to get the desired accuracy -- something like this:

N[f[SetPrecision[x, Infinity], 6]

Here's such an wrapper for a function:

Options[nEval] := {AccuracyGoal -> Automatic, "MaxExtraPrecision" -> Automatic};
nEval[f_, x_?NumericQ, OptionsPattern[]] := 
  Block[{$MaxExtraPrecision = 
     OptionValue["MaxExtraPrecision"] /. Automatic -> $MaxExtraPrecision},
   N[f[SetPrecision[x, Infinity]], OptionValue[AccuracyGoal] /. Automatic -> 6]
   ];

Then

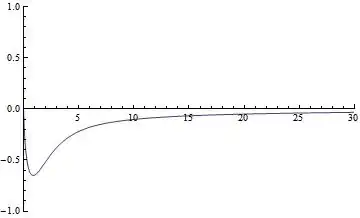
myF[x_] := CoshIntegral[x] Sinh[x] - Cosh[x] SinhIntegral[x];

Plot[nEval[myF, x], {x, 0, 30}, PlotRange -> {{0, 30}, {-1, 1}}]

Mathematica graphics

The precision is adapted to what is needed.

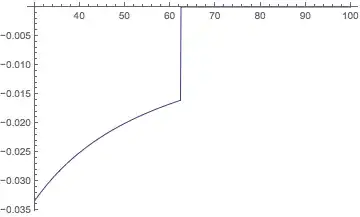
Plot[nEval[myF, x], {x, 30, 60}, PlotRange -> {Automatic, {-0.35, 0}}]

Mathematica graphics

But one can still get a catastrophic loss of precision, due to the limit $MaxExtraPrecision.

Plot[nEval[myF, x], {x, 30, 100}, PlotRange -> {Automatic, {-0.35, 0}}]

Mathematica graphics

In that case, one can raise the amount of extra precision allowed, even to Infinity. (In some cases, it might take an exorbitant amount of time to finish, but in this case, it is still quick.)

Plot[nEval[myF, x, "MaxExtraPrecision" -> Infinity], {x, 30, 100}, 
 PlotRange -> {Automatic, {-0.35, 0}}]

Mathematica graphics

score 2 · Answer 4 · answered Dec 13 '13 at 19:15

A bit of an aside, but the limit behavior of this expression has a readily found simple form:

Simplify[Re@ 
 (*the series expansion has an imaginary part that asymptotically vanishes*)
         Normal@Series[
              CoshIntegral[x] Sinh[x] - SinhIntegral[x] Cosh[x],
                 {x, Infinity, 3}], Assumptions -> {x > 0}]

(* -(2+x^2)/x^3 *)

Now you can plot w/o using excessive precision:

Plot[Piecewise[ {
   {CoshIntegral[x] Sinh[x] - SinhIntegral[x] Cosh[x], x < 10},
   {-((2 + x^2)/x^3), True}
      }], {x, 0, 30},  PlotRange -> All ]

Numerical instability in cosh and sinh - integral functions

4 Answers4

Linked