Plotting Voxel in mathematica

Question

I am developping a 3D reconstruction application. I recuperate the voxels coordinates (the coordinate of each voxel) of the object that I need to reconstruct. Each voxel have a dimensions like this 5cm*5cm*5cm. I need to reconstruct this volume. I try to use Image3D function by put just a 3d binary table representing the voxels that belongs to volume but I could not change the size of each voxel. Any help please?

The size of every voxel in a grid is always the same, by definition. — ssch, Dec 16 '13 at 21:53
@ssch, yes of course, In my case, the dimension of each pixel is 5cm5cm5cm. What is wrong? — phdstudent, Dec 16 '13 at 22:05
Add a link to your data @phdstudent. That will automagically make your question more appealing :) — stathisk, Dec 16 '13 at 22:45
The absolute size of your voxels only matters if you are combining with other graphics. What problem are you having specifically? — george2079, Dec 18 '13 at 00:27
I suspect you'll get best performance if you stick with Image3D. Scale everything else into the unit voxel space defined by the image. Or cross your fingers, maybe soon Wolfram will give us Inset3D..:-) — george2079, Dec 18 '13 at 20:14

Yves Klett · Accepted Answer · 2013-12-17T15:48:50.797

Another way to get pseudo-voxels using Cuboid (mainly for versions <9):

{dx, dy, dz} = {5, 5, 5};

Graphics3D[
 Table[{EdgeForm[], Opacity[.1], Hue[Sqrt[x^2 + y^2 + z^2]/25], 
   Cuboid[{x, y, z} - {dx, dy, dz}/2, {x, y, z} + {dx, dy, dz}/
      2]}, {x, -25, 25, dx}, {y, -25, 25, dy}, {z, -25, 25, dz}]]

Mathematica graphics

or using other increments:

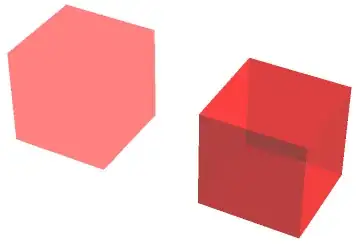
Mathematica graphics

... and just to give an impression of the visual differences between Raster3D (left) and Cuboid (right):

Graphics3D[{Opacity[.5], Raster3D[{{{{1, 0, 0}}}}], EdgeForm[None], 
Red, Cuboid[{2, 0, 0}]}, Lighting -> "Neutral", Boxed -> False]

Mathematica graphics

chuy · Answer 2 · 2013-12-17T22:09:47.633

3

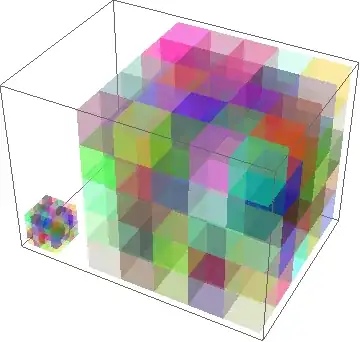
Using Raster3D :

Graphics3D[{Opacity[.5],Raster3D[RandomReal[1,{5,5,5,3}]]}, Axes-> True]

unit voxel

This will generate unit voxels, while the following creates 5x5x5 unit voxels:

Graphics3D[{Opacity[.5],Raster3D[RandomReal[1,{5,5,5,3}],{{0,0,0},{25,25,25}}]}, Axes-> True]

5x5x5 voxels

Perhaps this will clarify the sizes:

Show[{
Graphics3D[{Opacity[.5],Raster3D[RandomReal[1,{5,5,5,3}]]}],
Graphics3D[{Opacity[.5],Raster3D[RandomReal[1,{5,5,5,3}],{{10,0,0},{35,25,25}}]}]
}]

enter image description here

edited Dec 17 '13 at 22:09

answered Dec 17 '13 at 15:01

chuy

11,205
28
48

What is the relation between my question and your solution? – phdstudent Dec 17 '13 at 17:02
1

@phdstudent you were asking 5x5x5 voxels, right? – Yves Klett Dec 17 '13 at 21:57
@YvesKlett What is the information illustrated by RandomReal[1,{5,5,5,3}] ? Is this matrix contains the center or the opposite corner of each voxel or… what? – phdstudent Dec 17 '13 at 22:54
@phdstudent please look up the documentation for Raster3D, esp. under Scope->Specification. – Yves Klett Dec 18 '13 at 07:57

score 1 · Answer 3 · answered Dec 17 '13 at 05:08

1

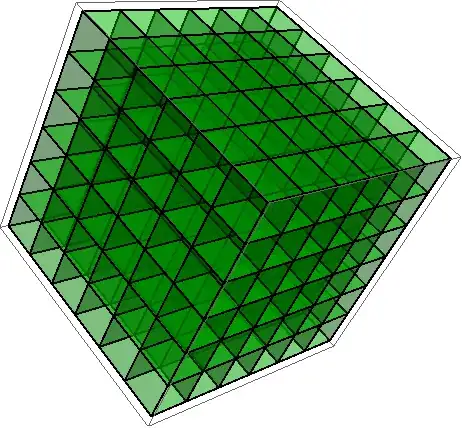
Here is the code for Plotting voxel grid:

   PlottingVoxel[{VoxCenter_, VoxH_, VoxL_, VoxP_}] := 
   Module[{Ip, CoordVox}, (
  Ip = VoxCenter - N[{VoxH/2, VoxL/2, VoxP/2}];
  CoordVox = {{Ip, Ip + {VoxH, 0, 0}, Ip + {VoxH, VoxP, 0}, 
  Ip + {0, VoxP, 0}},
  {Ip, Ip + {VoxH, 0, 0}, Ip + {VoxH, 0, VoxL}, 
  Ip + {0, 0, VoxL}},
  {Ip + {0, 0, VoxL}, Ip + {VoxH, 0, VoxL}, 
  Ip + {VoxH, VoxL, VoxL}, Ip + {0, VoxP, VoxL}},
  {Ip + {0, 0, VoxL}, Ip + {0, VoxP, VoxL}, Ip + {0, VoxP, 0}, 
  Ip},
   {Ip + {0, VoxP, 0}, Ip + {VoxH, VoxP, 0}, 
  Ip + {VoxH, VoxP, VoxL}, Ip + {0, VoxP, VoxL}},
  {Ip + {VoxH, 0, 0}, Ip + {VoxH, VoxP, 0}, 
  Ip + {VoxH, VoxP, VoxL}, Ip + {VoxH, 0, VoxL}}};
  Polygon[CoordVox]

  )]

  Note:
  VoxCenter=center of voxel.
  VoxH,VoxL,VoxP is the dimension of the voxel.

Exemple:

 Graphics3D[{FaceForm[Green], EdgeForm[Thick], Opacity[0.3], 
 PlottingVoxel[{#, 1, 1, 1}] & /@ 
 Flatten[Table[{x, y, z}, {x, 0, 5}, {y, 0, 5}, {z, 0, 5}], 2], 
 FaceForm[Blue], Opacity[.4]}]

Result: enter image description here

answered Dec 17 '13 at 05:08

phdstudent

423
3
12

Those are not really voxels, though. To similar effect, you could use Cuboid (e.g. cribbed from the docs: Graphics3D[ Table[{EdgeForm[], Opacity[.1], Hue[RandomReal[]], Cuboid[RandomReal[4, 3]]}, {40}]] ) – Yves Klett Dec 17 '13 at 08:11
@YvesKlett, Why did you say that my solution is not a real voxels? I do not understand the difference? I used the polygon to make a cuboid and you used the cuboid directly. – phdstudent Dec 17 '13 at 15:19
Another things, I try your solution and it get the same excution time that my own!Please do you can try the code for a grid with dimensions 300,300,300 and the diemension of each voxels is 555? – phdstudent Dec 17 '13 at 15:27
From a rendering point, a cuboid set of polygon faces is not the same as a voxel (think ray-tracing). – Yves Klett Dec 17 '13 at 15:27
Ok! may be you are right! I have not a deep idea about ray tracing. But, How can I fix the computation problem? – phdstudent Dec 17 '13 at 15:30
My version will not differ much in terms of performance.I would recommend to go with @chuy´s solution, which is the way to go starting with V9. – Yves Klett Dec 17 '13 at 15:32

Plotting Voxel in mathematica

3 Answers3

Linked