3

There is a Business Cycles Map on Phaser 3.0 and I've trying to run it on Mathematica the last four days without succes.

The equations are

$$ x_1 = (1.0 - a s)x_1 + a \left[s m + g \left(\frac{s m}{d} - x_2\right) + \mathrm{atan}(x_1 - m)\right], $$ $$ x_2 = (1.0 - d)x_2 + s m + g \left(\frac{s m}{d} - x_2\right) + \mathrm{atan}(x_1 - m) $$

with the initial conditions

$$ t = 0, \quad x_1 = 17, \quad x_2 = 30, $$ and $$ a = 8.0, \quad d = 0.2, \quad g = 0.4, \quad m = 15, \quad s = 0.4. $$

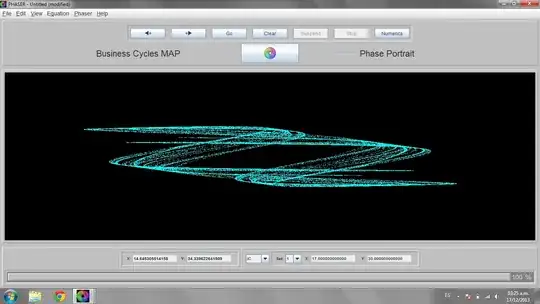
How it is showed on Phaser

I'd just copy the result on Phaser, but i have the trial version. The code I thought it could work is this:

a = 8.0; d = 0.2; g = 0.4; m = 15; s = 0.4;
x[0] := 17; y[0] := 30;
x[t_] := x[t] = (1.0 - a s) x[t - 1] + 
   a (s m + (g*(((s m)/d) - y[t - 1])) + ArcTan[x[t - 1] - m])
y[t_] := y[t] = (1.0 - d) y[t - 1] + s m + (g*((s m)/d) - y[t - 1]) + 
   ArcTan[x[t - 1] - m]
data = Table[{x[t], y[t]}, {t, 0, 100}];
ListPlot[data, AxesLabel -> {"x[t]", "y[t]"}, Joined -> False, 
 PlotRange -> {{0, 30}, {25, 35}}, Mesh -> Full, PlotMarkers -> None]

But it doesn't. Any suggestions?

J. M.'s missing motivation
  • 124,525
  • 11
  • 401
  • 574
  • 2
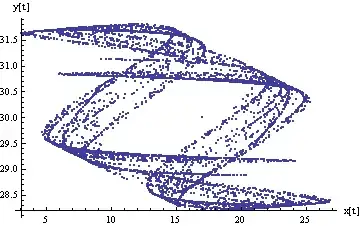
    But it doesn't in what sense? can you explain what does not work mean here? – Nasser Dec 17 '13 at 09:59
  • I think you have an interesting question in this, but I don't find it sufficiently well formed. If you can provide us with a description of what Phaser 3.0 does and how we can replicate what you have done in it, that will give us a better chance of helping. I even downloaded Phaser 3.0 to try and do this myself, but the version for OS X appears corrupted and won't install. Also, your Mathematica functions need more thought. You have functions calling themselves within their definitions. At 1st glance that looks problematic. I'll give it more thought, but a bit more from you will help. – Jagra Dec 17 '13 at 15:41
  • Nasser the points plotted have explosive behaviour, and jump into negative quadrants, which in this model is impossible. @Jagra I'm conscious that the functions need more thought, but the same code worked when I simulated the Discrete Predator-Prey model. The only Phaser description of waht it does is solving by iteration, sorry. –  Dec 17 '13 at 18:07

1 Answers1

6

Edit

You had an error in the transcription of the equation for y[t]:

a = 8.0; d = 0.2; g = 0.4; m = 15; s = 0.4;
data = RecurrenceTable[{x[0] == 17, y[0] == 30,
    x[t] == (1. - a s) x[t - 1] + a (s m + (g*(s m/d - y[t - 1])) + ArcTan[x[t - 1] - m]), 
    y[t] == (1. - d) y[t - 1] + s m + g*(s m/d - y[t - 1]) + ArcTan[x[t - 1] - m]}, {x, y}, 
    {t, 0, 7000}];
ListPlot[data, AxesLabel -> {"x[t]", "y[t]"}, PlotRange -> All,PlotStyle -> PointSize[Small]]

Mathematica graphics

Dr. belisarius
  • 115,881
  • 13
  • 203
  • 453
  • Could you provide a bit of explanation of your code. It has a lot of interesting things in it. +1 – Jagra Dec 17 '13 at 17:16
  • I never had occasion to use RecurrenceTable, so its syntax using equations seemed unfamiliar. A little explanation of how RecurrenceTable and any similarly structured functions work could help we uninitiated, better understand your solution. Its a very cool solution you've crafted. Knowing a bit of your thought on why you chose to attack the problem as you did, rather than some other way (Mathematica always seems to have other ways), would make for some interesting insights. Just curious ;-) – Jagra Dec 17 '13 at 18:28
  • @belisarius I really appreciate your time for answering. I think this allows us to explore the models possibilities, keep wondering why doesn't show the same plot? –  Dec 17 '13 at 18:30
  • @Jagra Those are recurrence equations. Mathematica has two functions to deal with them in a natural way: RSolve[] and RecurrenceTable[] ... and RSolve doesn't work in this case – Dr. belisarius Dec 17 '13 at 19:28
  • @belisarius I don't know if that's the case, because the model it's supposed to generate self sustaining cycles. And as I said, for the Discrete Predator-Prey it worked, so there must be something we are losing. –  Dec 17 '13 at 21:37
  • @IsaiasCordova See edit, please – Dr. belisarius Dec 18 '13 at 01:48
  • Many thanks for the explanation. – Jagra Dec 18 '13 at 01:57
  • @belisarius Oh man, I can't believe I screwed it on that. Thank you very much. For further reference, this is a model based on post keynesian Kaldor's thoughts (1940). –  Dec 18 '13 at 05:20