Kramers Kronig Relation for Phase and Complex Reflectivity

Question

I am a new user to Mathematica and I have been trying to figure out how to find $\Theta(\omega)$ from my 'experimental' values of energy and $\ln(\sqrt{R(\omega)})$ (I am just running a simulation, letting $R$ to be a Lorentizan curve and energy be $0\,\text{eV}$--$10\,\text{eV}$, with $0.001$ interval). The following are the equations I used:

$$ \ln(r(\omega)) = \ln\left(\sqrt{R(\omega)}\right) + \mathrm{i}\,\Theta(\omega) $$

and by KK relation,

$$ \Theta(\omega) = -\frac{\omega}{\pi} \int_{0}^{\infty}\frac{\ln\left(\sqrt{R(x)}\right) - \ln\left(\sqrt{R(ω)}\right)}{x^2-\omega^2}\,\mathrm{d}x, $$

These equations can be found from this website: http://dept.phy.bme.hu/education/optical_spectroscopy/lecture2_rev.pdf (pg5) and the physical meaning of $R$ is the reflectivity, and $\Theta(\omega)$ is the phase difference between $R$ and $r$, the reflection coeffecient.

The following is my 'data'. http://pastebin.com/VfLDk7Lh. The data is already in $\ln(\sqrt{R})$, energy.

Here is the code that I have keyed into mathematica.

{Reflec, w} = ToExpression@Import["C:\\Users\\user\\Desktop\\1.txt"];

f = Interpolation[Transpose[{Flatten[w], Flatten[Reflec]}]]

delta[w_] := 
delta[w] = -2 w/Pi NIntegrate[(f[a] - f[w])/(a^2 - w^2), {a, 0, 10}, 
Method -> "PrincipalValue", Exclusions -> {(a^2 - w^2) == 0}] // 
Quiet

Table[delta[w], {w, 0, 10, 0.1}]

Mathematica is able to give me some values $\Theta(\omega)$. However, when I calculated the dielectric $\varepsilon_2$ with another program IGOR, there are some negatives values. Hence, I would like to find out if there are anything wrong with the commands I typed in Mathematica.

Please post your experimental values somewhere, for example on Pastebin.com. What is its physical meaning exactly? — Alexey Popkov, Dec 20 '13 at 10:50
You are using the Quiet command -- this suppresses warnings about what things that might be misbehaving. Try removing Quiet and see if there are any warnings. — bill s, Dec 20 '13 at 14:25
@ Alexey Popkov Hi, thanks for your reply. I edited my post and added the values too. — user11251, Dec 21 '13 at 00:46
@ bills Hi I have tried removing Quiet command but there is not much of a difference. I suspect that there is something wrong with the Nintegrate command that I typed, but I cannot figure this out. Thanks. — user11251, Dec 21 '13 at 00:48
Is there any particular reason for retaining the {{value},{value},...} structure for w? — Peltio, Dec 22 '13 at 14:07

score 4 · Accepted Answer · edited Apr 13 '17 at 12:55

First of all, you should specify Exclusions using RuleDelayed (:>) if it contains global symbols. Secondly, by default Interpolation uses Hermite interpolation of order 3. This order is too high and can introduce artifacts which make NIntegrate difficult to achieve the desired precision. The dense of the points is high in your case, so I recommend to use linear interpolation (InterpolationOrder -> 1). But it still does not solve the problem. You need to play with the Method options in order to get it working. It seems that in your case this approach works:

f = Interpolation[Transpose[{Flatten[w], Flatten[Reflec]}], InterpolationOrder -> 1]
ClearAll[delta];
delta[w_] := 
 delta[w] = -2 w/Pi NIntegrate[(f[a] - f[w])/(a^2 - w^2), {a, 0, 10}, 
    Method -> {"TrapezoidalRule", "Points" -> Length[w]}, 
    MaxRecursion -> 0]

Table[delta[w], {w, 0, 10, 1}]

< skipped error messages >

{0.,-0.587782,-0.98002,-0.297634,1.31909,1.30856,1.24664,1.18417,1.12557,1.07209,1.02361}

Let us compare it with corrected version of your original code:

f = Interpolation[Transpose[{energy, ln}], InterpolationOrder -> 1]
ClearAll[delta];
delta[w_] := 
 delta[w] = -2 w/Pi NIntegrate[(f[a] - f[w])/(a^2 - w^2), {a, 0, 10}, 
    Method -> "PrincipalValue", Exclusions :> {(a^2 - w^2) == 0}]

Table[delta[w], {w, 0, 10, 1}]

< skipped error messages >

{0., -0.587836, -0.980125, -0.297634, 1.31919, 1.30868, 1.24667, 1.1842, 1.12559, 1.0721, 1.02362}

The result is almost identical but the messages in the case of Method -> "PrincipalValue" are very disappointing and indicate that the result is completely unreliable while with suggested solution they just say that the accuracy is low but there is no indication that even its sign is unreliable.

=== UPDATE START ===

I just have found in the Documentation how to combine both approaches. The following code gives huge speedup and much lesser number of error messages (note that I have dropped Exclusions and inserted the singular point directly in the range specification):

f = Interpolation[Transpose[{energy, ln}], InterpolationOrder -> 1]
ClearAll[delta];
delta[w_] := 
 delta[w] = -2 w/Pi NIntegrate[(f[a] - f[w])/(a^2 - w^2), {a, 0, w, 10}, 
           Method -> {"PrincipalValue", "SingularPointIntegrationRadius" -> .01,
              Method -> {"TrapezoidalRule"}}]

Table[delta[w], {w, 0, 10, 1}]

< skipped error messages >

{0.,-0.587836,-0.980126,-0.297633,1.31919,1.30868,1.24667,1.1842,1.12559,1.0721,1.02362}

And switching to the "LocalAdaptive" strategy removes almost all the error messages and gives even better performance:

f = Interpolation[Transpose[{energy, ln}], InterpolationOrder -> 1];
ClearAll[delta];
delta[w_] := 
 delta[w] = -2 w/
    Pi NIntegrate[(f[a] - f[w])/(a^2 - w^2), {a, 0, w, 10}, 
    Method -> {"PrincipalValue", 
      "SingularPointIntegrationRadius" -> .01, 
      Method -> {"LocalAdaptive", Method -> {"TrapezoidalRule"}}}]

Table[delta[w], {w, 0, 10, 1}]

NIntegrate::ncvb: NIntegrate failed to converge to prescribed accuracy after 9 recursive bisections in a near {a} = {6.51455*10^-16}. NIntegrate obtained 9.623894093883607 and 0.007834853650777518 for the integral and error estimates. >>

{0.,-0.587836,-0.980126,-0.297634,1.31919,1.30867,1.24667,1.18419,1.12559,1.0721,1.02362}

If you need to compute points with lesser step, you should lower the value of the "SingularPointIntegrationRadius" suboption (probably at least 10 times smaller than the step).

=== UPDATE END ===

=== UPDATE 2 START ===

Incorporating this idea, the problem also can be solved in the following way:

f = Interpolation[Transpose[{energy, ln}], InterpolationOrder -> 1];
ClearAll[delta];
delta[w_] := 
 delta[w] = -2 w/
    Pi NIntegrate[(f[a] - f[w])/(a^2 - w^2), {a, 0, w, 10}, 
    Method -> {"PrincipalValue", "SingularPointIntegrationRadius" -> .01, 
      Method -> {"InterpolationPointsSubdivision", "MaxSubregions" -> 10^9}}]

Table[delta[w], {w, 0, 10, 1}]

< skipped error messages >

{0.,-0.587835,-0.980125,-0.297634,1.31919,1.30868,1.24667,1.1842,1.12559,1.0721,1.02362}

As earlier, switching to the "LocalAdaptive" strategy with "TrapezoidalRule" rule removes almost all the error messages:

f = Interpolation[Transpose[{energy, ln}], InterpolationOrder -> 1];
ClearAll[delta];
delta[w_] := 
 delta[w] = -2 w/
    Pi NIntegrate[(f[a] - f[w])/(a^2 - w^2), {a, 0, w, 10}, 
    Method -> {"PrincipalValue", "SingularPointIntegrationRadius" -> .01, 
      Method -> {"InterpolationPointsSubdivision", "MaxSubregions" -> 10^9, 
        Method -> {"LocalAdaptive", Method -> {"TrapezoidalRule"}}}}]

Table[delta[w], {w, 0, 10, 1}]

During evaluation of In[163]:= NIntegrate::ncvb: NIntegrate failed to converge to prescribed accuracy after 9 recursive bisections in a near {a} = {6.68521*10^-16}. NIntegrate obtained 6.589303369962569 and 0.006663527436642447 for the integral and error estimates. >>

{0., -0.587835, -0.980125, -0.297634, 1.31919, 1.30868, 1.24667, 1.1842, 1.12559, 1.0721, 1.02361}

=== UPDATE 2 END ===

As I show in the linked question, in the cases like your the best way is to take the integral directly by substituting linear function between successive datapoints instead of f. Here I give you just starting point, not a complete solution:

Integrate[b*(a - w)/(a^2 - w^2), {a, a1, a2}, 
 Assumptions -> b \[Element] Reals && 0 <= a1 <= w <= a2, 
 PrincipalValue -> True]

b Log[(a2+w)/(a1+w)]

Here a1 and a2 are successive points from the w list, b*(a - w) is a linear interpolation function for f[a] - f[w] between a1 and a2 (finding coefficient b is trivial task). The complete integral will be equal to the sum of integrals between successive data points. (I have not carefully checked the code, I just hope you will get the idea.)

@ Alexey Popkov Thank you so much for that elaborated explanation. However, being a new user to mathematica, I have difficulties understanding the last part on the substitution of linear function. Do you mind explaining more? Also, what does a0 mean and how do we find a0? — user11251, Dec 22 '13 at 11:55
@user11251 The last part contains explanation of another approach which is formally mathematically identical but assumes that the user will make the work of NIntegrate by yourself (with little help from Integrate) and reformulate the programmatic problem as explicit summation of closed-form integrals between successive datapoints. a0 was a mistake since in f[a] - f[w] the free term will be canceled (f[x] is replaced by a0 + b*x where a0 is free term, b is the slope). — Alexey Popkov, Dec 22 '13 at 12:03

user11251 · Answer 2 · 2014-01-06T06:50:56.017

points={{0,-3.40175},{0.1,-3.36789},{0.2,-3.33284},{0.3,-3.29652},{0.4,-3.25884},{0.5,-3.21968},{0.6,-3.17892},{0.7,-3.13644},{0.8,-3.09207},{0.9,-3.04566},{1,-2.99698},{1.1,-2.94582},{1.2,-2.89191},{1.3,-2.83494},{1.4,-2.77454},{1.5,-2.71027},{1.6,-2.6416},{1.7,-2.5679},{1.8,-2.48837},{1.9,-2.40201},{2,-2.30756},{2.1,-2.20336},{2.2,-2.08719},{2.3,-1.95601},{2.4,-1.80546},{2.5,-1.62905},{2.6,-1.41661},{2.7,-1.15129},{2.8,-0.804719},{2.9,-0.346574},{3,0},{3.1,-0.346574},{3.2,-0.804719},{3.3,-1.15129},{3.4,-1.41661},{3.5,-1.62905},{3.6,-1.80546},{3.7,-1.95601},{3.8,-2.08719},{3.9,-2.20336},{4,-2.30756},{4.1,-2.40201},{4.2,-2.48837},{4.3,-2.5679},{4.4,-2.6416},{4.5,-2.71027},{4.6,-2.77454},{4.7,-2.83494},{4.8,-2.89191},{4.9,-2.94582},{5,-2.99823},{5.1,-3.0469},{5.2,-3.09331},{5.3,-3.13767},{5.4,-3.18014},{5.5,-3.22087},{5.6,-3.26002},{5.7,-3.29769},{5.8,-3.33399},{5.9,-3.36902},{6,-3.40286},{6.1,-3.4356},{6.2,-3.4673},{6.3,-3.49802},{6.4,-3.52783},{6.5,-3.55678},{6.6,-3.58491},{6.7,-3.61227},{6.8,-3.6389},{6.9,-3.66484},{7,-3.69013},{7.1,-3.71479},{7.2,-3.73886},{7.3,-3.76236},{7.4,-3.78533},{7.5,-3.80777},{7.6,-3.82973},{7.7,-3.85121},{7.8,-3.87224},{7.9,-3.89284},{8,-3.91302},{8.1,-3.93281},{8.2,-3.95221},{8.3,-3.97123},{8.4,-3.98991},{8.5,-4.00824},{8.6,-4.02624},{8.7,-4.04393},{8.8,-4.06131},{8.9,-4.07839},{9,-4.09518},{9.1,-4.11169},{9.2,-4.12794},{9.3,-4.14393},{9.4,-4.15966},{9.5,-4.17516},{9.6,-4.19041},{9.7,-4.20544},{9.8,-4.22024},{9.9,-4.23483},{10,-4.24921}};

f=Interpolation[points, InterpolationOrder->1];
tetha[w_]:=tetha[w]=-2w/Pi NIntegrate[(f[a] - f[w])/(a^2-w^2),{a,0,10},Method->"PrincipalValue",Exclusions->{(a^2-w^2)==0}]//Quiet

Column[Table[tetha[w],{w,0,10,0.1}]]

So this is what I came up with; I skipped your suggestion of using linear interpolation as it seemed like too much work for my experimental data. Here I did it with 100 points of my data and it gave me quite a decent imaginary epsilon shape. (the general shape is correct, but there are artifacts as you can see below)

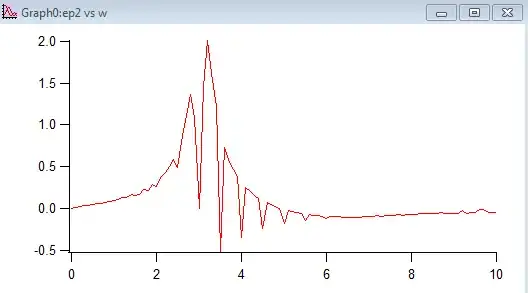
enter image description here

I noticed though that they are at every 0.5 interval starting at 3.0 (3.5, 4.0, 4.5...) And was hoping you could maybe help me in fine tuning my formula or at least pointing out what is causing these artifacts? Is it the interpolation order that's causing this?

Many thanks and gratitude. Cheers.

Update start

points={{0,0.110988},{0.1,0.118765},{0.2,0.127389},{0.3,0.136986},{0.4,0.14771},{0.5,0.159744},{0.6,0.17331},{0.7,0.188679},{0.8,0.206186},{0.9,0.226244},{1,0.249377},{1.1,0.276243},{1.2,0.307692},{1.3,0.344828},{1.4,0.389105},{1.5,0.442478},{1.6,0.507614},{1.7,0.588235},{1.8,0.689655},{1.9,0.819672},{2,0.990099},{2.1,1.21951},{2.2,1.53846},{2.3,2},{2.4,2.7027},{2.5,3.84615},{2.6,5.88235},{2.7,10},{2.8,20},{2.9,50},{3,100},{3.1,50},{3.2,20},{3.3,10},{3.4,5.88235},{3.5,3.84615},{3.6,2.7027},{3.7,2},{3.8,1.53846},{3.9,1.21951},{4,0.990099},{4.1,0.819672},{4.2,0.689655},{4.3,0.588235},{4.4,0.507614},{4.5,0.442478},{4.6,0.389105},{4.7,0.344828},{4.8,0.307692},{4.9,0.276243},{5,0.248755},{5.1,0.225681},{5.2,0.205676},{5.3,0.188217},{5.4,0.17289},{5.5,0.159362},{5.6,0.147362},{5.7,0.136668},{5.8,0.127097},{5.9,0.118497},{6,0.110742},{6.1,0.103723},{6.2,0.0973518},{6.3,0.0915497},{6.4,0.0862513},{6.5,0.0813999},{6.6,0.0769466},{6.7,0.072849},{6.8,0.0690702},{6.9,0.065578},{7,0.062344},{7.1,0.0593436},{7.2,0.0565546},{7.3,0.0539577},{7.4,0.0515357},{7.5,0.0492732},{7.6,0.0471564},{7.7,0.0451732},{7.8,0.0433125},{7.9,0.0415644},{8,0.0399201},{8.1,0.0383715},{8.2,0.0369112},{8.3,0.0355328},{8.4,0.0342301},{8.5,0.0329978},{8.6,0.0318309},{8.7,0.0307248},{8.8,0.0296753},{8.9,0.0286787},{9,0.0277315},{9.1,0.0268305},{9.2,0.0259727},{9.3,0.0251553},{9.4,0.024376},{9.5,0.0236323},{9.6,0.0229221},{9.7,0.0222435},{9.8,0.0215945},{9.9,0.0209736},{10,0.020379}};
f=Interpolation[points];

ep1[w_]:=ep1[w]=1+2/Pi NIntegrate[(a f[a])/(a^2-w^2),{a,0,10},Method->"PrincipalValue",Exclusions->{(a^2-w^2)==0}]//Quiet

Plot[ep1[w],{w,0,10},AxesOrigin->{0,0},PlotRange->{{0,10},{-90,90}}]

I tried doing another simulation of lorentzian ep2 to ep1. This is the code i used to get the correct curve ep1 here, as backed up in many online resources. enter image description here

and the below is the code i used using your suggestion.

points = {{0, 0.110988}, {0.1, 0.118765}, {0.2, 0.127389}, {0.3,
    0.136986}, {0.4, 0.14771}, {0.5, 0.159744}, {0.6, 0.17331}, {0.7, 
    0.188679}, {0.8, 0.206186}, {0.9, 0.226244}, {1, 0.249377}, {1.1, 
    0.276243}, {1.2, 0.307692}, {1.3, 0.344828}, {1.4, 
    0.389105}, {1.5, 0.442478}, {1.6, 0.507614}, {1.7, 
    0.588235}, {1.8, 0.689655}, {1.9, 0.819672}, {2, 0.990099}, {2.1, 
    1.21951}, {2.2, 1.53846}, {2.3, 2}, {2.4, 2.7027}, {2.5, 
    3.84615}, {2.6, 5.88235}, {2.7, 10}, {2.8, 20}, {2.9, 50}, {3, 
    100}, {3.1, 50}, {3.2, 20}, {3.3, 10}, {3.4, 5.88235}, {3.5, 
    3.84615}, {3.6, 2.7027}, {3.7, 2}, {3.8, 1.53846}, {3.9, 
    1.21951}, {4, 0.990099}, {4.1, 0.819672}, {4.2, 0.689655}, {4.3, 
    0.588235}, {4.4, 0.507614}, {4.5, 0.442478}, {4.6, 
    0.389105}, {4.7, 0.344828}, {4.8, 0.307692}, {4.9, 0.276243}, {5, 
    0.248755}, {5.1, 0.225681}, {5.2, 0.205676}, {5.3, 
    0.188217}, {5.4, 0.17289}, {5.5, 0.159362}, {5.6, 0.147362}, {5.7,
     0.136668}, {5.8, 0.127097}, {5.9, 0.118497}, {6, 0.110742}, {6.1,
     0.103723}, {6.2, 0.0973518}, {6.3, 0.0915497}, {6.4, 
    0.0862513}, {6.5, 0.0813999}, {6.6, 0.0769466}, {6.7, 
    0.072849}, {6.8, 0.0690702}, {6.9, 0.065578}, {7, 0.062344}, {7.1,
     0.0593436}, {7.2, 0.0565546}, {7.3, 0.0539577}, {7.4, 
    0.0515357}, {7.5, 0.0492732}, {7.6, 0.0471564}, {7.7, 
    0.0451732}, {7.8, 0.0433125}, {7.9, 0.0415644}, {8, 
    0.0399201}, {8.1, 0.0383715}, {8.2, 0.0369112}, {8.3, 
    0.0355328}, {8.4, 0.0342301}, {8.5, 0.0329978}, {8.6, 
    0.0318309}, {8.7, 0.0307248}, {8.8, 0.0296753}, {8.9, 
    0.0286787}, {9, 0.0277315}, {9.1, 0.0268305}, {9.2, 
    0.0259727}, {9.3, 0.0251553}, {9.4, 0.024376}, {9.5, 
    0.0236323}, {9.6, 0.0229221}, {9.7, 0.0222435}, {9.8, 
    0.0215945}, {9.9, 0.0209736}, {10, 0.020379}};
f = Interpolation[points];

ep1[w_] := 
 ep1[w] = 1 + 
   2/Pi NIntegrate[(a f[a])/(a^2 - w^2), {a, 0, w, 10}, 
     Method -> {"PrincipalValue", 
       "SingularPointIntegrationRadius" -> .01, 
       Method -> {"InterpolationPointsSubdivision", 
         "MaxSubregions" -> 10^9, 
         Method -> {"LocalAdaptive", Method -> {"TrapezoidalRule"}}}}]

Plot[ep1[w], {w, 0, 10}, AxesOrigin -> {0, 0}, 
 PlotRange -> {{0, 10}, {-90, 90}}]

which results in a similar but oddly graphed out curve, which I'm not sure if i should count as artifacts introduced by your method?

enter image description here

UPDATE 1 END

UPDATE 2 START

Hello, although it has been some time, I am still trying to figure this integration out. Currently, I'm trying to troubleshoot the integration which I hope you can enlighten me.

points={{0,-2.99573227355399},{0.1,-2.93492013415723},{0.2,-2.8724340572095},{0.3,-2.80819714970715},{0.4,-2.74212951475507},{0.5,-2.67414864942653},{0.6,-2.60417007061482},{0.7,-2.53210825127229},{0.8,-2.45787797740008},{0.9,-2.38139627341834},{1,-2.30258509299405},{1.1,-2.2213750375685},{1.2,-2.13771044980381},{1.3,-2.0515563381903},{1.4,-1.96290772542388},{1.5,-1.87180217690159},{1.6,-1.77833644889591},{1.7,-1.68268837417369},{1.8,-1.58514521986506},{1.9,-1.48613969608961},{2,-1.38629436111989},{2.1,-1.28647402583768},{2.2,-1.18784342239605},{2.3,-1.09192330051731},{2.4,-1.00063188030791},{2.5,-0.916290731874155},{2.6,-0.841567185678219},{2.7,-0.779324876800997},{2.8,-0.732367893713227},{2.9,-0.703097511413113},{3,-0.693147180559945},{3.1,-0.703097511413113},{3.2,-0.732367893713227},{3.3,-0.779324876800997},{3.4,-0.841567185678219},{3.5,-0.916290731874155},{3.6,-1.00063188030791},{3.7,-1.09192330051731},{3.8,-1.18784342239605},{3.9,-1.28647402583768},{4,-1.38629436111989},{4.1,-1.48613969608961},{4.2,-1.58514521986506},{4.3,-1.68268837417369},{4.4,-1.77833644889591},{4.5,-1.87180217690159},{4.6,-1.96290772542388},{4.7,-2.0515563381903},{4.8,-2.13771044980381},{4.9,-2.2213750375685},{5,-2.30258509299405},{5.1,-2.38139627341834},{5.2,-2.45787797740008},{5.3,-2.53210825127229},{5.4,-2.60417007061482},{5.5,-2.67414864942653},{5.6,-2.74212951475507},{5.7,-2.80819714970715},{5.8,-2.8724340572095},{5.9,-2.93492013415723},{6,-2.99573227355399},{6.1,-3.05494413318584},{6.2,-3.11262602502549},{6.3,-3.16884489126264},{6.4,-3.2236643416},{6.5,-3.27714473299218},{6.6,-3.32934327789417},{6.7,-3.38031417074573},{6.8,-3.43010872515658},{6.9,-3.47877551630753},{7,-3.52636052461616},{7.1,-3.57290727786152},{7.2,-3.61845698981739},{7.3,-3.66304869407941},{7.4,-3.70671937224227},{7.5,-3.74950407593037},{7.6,-3.79143604243903},{7.7,-3.83254680392635},{7.8,-3.87286629022695},{7.9,-3.91242292544947},{8,-3.95124371858143},{8.1,-3.98935434836447},{8.2,-4.02677924272633},{8.3,-4.06354165306706},{8.4,-4.0996637236997},{8.5,-4.13516655674236},{8.6,-4.17007027275024},{8.7,-4.20439406736606},{8.8,-4.23815626425418},{8.9,-4.27137436457029},{9,-4.30406509320417},{9.1,-4.33624444201875},{9.2,-4.36792771029438},{9.3,-4.39912954257354},{9.4,-4.42986396408804},{9.5,-4.46014441393783},{9.6,-4.48998377617897},{9.7,-4.51939440896669},{9.8,-4.54838817188911},{9.9,-4.57697645161731},{10,-4.60517018598809}};

f=Interpolation[points];

-0.1/Pi NIntegrate[(f[a])/(a^2-0.1^2),{a,0,0.1,10},Method->{"PrincipalValue"}]

is supposed to return me the result of tetha[0.1] as far as i know which mathematica computes out as -0.0892917.

However, when I try the column table method, i seem to get a different answer at tetha[0.1]. I know this might turn out to be a simple issue, my apologies in advance.

points={{0,-2.99573227355399},{0.1,-2.93492013415723},{0.2,-2.8724340572095},{0.3,-2.80819714970715},{0.4,-2.74212951475507},{0.5,-2.67414864942653},{0.6,-2.60417007061482},{0.7,-2.53210825127229},{0.8,-2.45787797740008},{0.9,-2.38139627341834},{1,-2.30258509299405},{1.1,-2.2213750375685},{1.2,-2.13771044980381},{1.3,-2.0515563381903},{1.4,-1.96290772542388},{1.5,-1.87180217690159},{1.6,-1.77833644889591},{1.7,-1.68268837417369},{1.8,-1.58514521986506},{1.9,-1.48613969608961},{2,-1.38629436111989},{2.1,-1.28647402583768},{2.2,-1.18784342239605},{2.3,-1.09192330051731},{2.4,-1.00063188030791},{2.5,-0.916290731874155},{2.6,-0.841567185678219},{2.7,-0.779324876800997},{2.8,-0.732367893713227},{2.9,-0.703097511413113},{3,-0.693147180559945},{3.1,-0.703097511413113},{3.2,-0.732367893713227},{3.3,-0.779324876800997},{3.4,-0.841567185678219},{3.5,-0.916290731874155},{3.6,-1.00063188030791},{3.7,-1.09192330051731},{3.8,-1.18784342239605},{3.9,-1.28647402583768},{4,-1.38629436111989},{4.1,-1.48613969608961},{4.2,-1.58514521986506},{4.3,-1.68268837417369},{4.4,-1.77833644889591},{4.5,-1.87180217690159},{4.6,-1.96290772542388},{4.7,-2.0515563381903},{4.8,-2.13771044980381},{4.9,-2.2213750375685},{5,-2.30258509299405},{5.1,-2.38139627341834},{5.2,-2.45787797740008},{5.3,-2.53210825127229},{5.4,-2.60417007061482},{5.5,-2.67414864942653},{5.6,-2.74212951475507},{5.7,-2.80819714970715},{5.8,-2.8724340572095},{5.9,-2.93492013415723},{6,-2.99573227355399},{6.1,-3.05494413318584},{6.2,-3.11262602502549},{6.3,-3.16884489126264},{6.4,-3.2236643416},{6.5,-3.27714473299218},{6.6,-3.32934327789417},{6.7,-3.38031417074573},{6.8,-3.43010872515658},{6.9,-3.47877551630753},{7,-3.52636052461616},{7.1,-3.57290727786152},{7.2,-3.61845698981739},{7.3,-3.66304869407941},{7.4,-3.70671937224227},{7.5,-3.74950407593037},{7.6,-3.79143604243903},{7.7,-3.83254680392635},{7.8,-3.87286629022695},{7.9,-3.91242292544947},{8,-3.95124371858143},{8.1,-3.98935434836447},{8.2,-4.02677924272633},{8.3,-4.06354165306706},{8.4,-4.0996637236997},{8.5,-4.13516655674236},{8.6,-4.17007027275024},{8.7,-4.20439406736606},{8.8,-4.23815626425418},{8.9,-4.27137436457029},{9,-4.30406509320417},{9.1,-4.33624444201875},{9.2,-4.36792771029438},{9.3,-4.39912954257354},{9.4,-4.42986396408804},{9.5,-4.46014441393783},{9.6,-4.48998377617897},{9.7,-4.51939440896669},{9.8,-4.54838817188911},{9.9,-4.57697645161731},{10,-4.60517018598809}};

f=Interpolation[points];
tetha[w_]:=
tetha[w]=-w/Pi NIntegrate[(f[a])/(a^2-w^2),{a,0,w,10},Method->{"PrincipalValue"}]

Column[Table[tetha[w],{w,0,10,0.1}]]

which returns me a value of tetha[0.1]=-0.0799477. Could you please help me enlighten why is this so? The method of solving the principalvalue is kept the same in both cases.

I cannot reproduce your plot with Mathematica 8.0.4. There are lots of error messages and in many cases NIntegrate cannot give numerical result at all. — Alexey Popkov, Dec 23 '13 at 14:47
hey thanks for the reply. this plot is for imaginary ep2, which is computed using the tetha gotten in mathematica and my known R. the known relationship is lnr = ln(SqrtR) + i(tetha) and epsilon = ep1 +i(ep2) = (1-r)^2/(1+r)^2 and yes there were alot of error messages in the Nintegrate, but I ignored them. — user11251, Dec 24 '13 at 03:17
Have you seen the update section in my answer? I think I have solved your problem. — Alexey Popkov, Dec 24 '13 at 09:20
merry christmas and thank you once again. the integration is error free, but the integration results is wrong. the results do not reproduce those reported in journals. :( — user11251, Dec 26 '13 at 11:58
I do not think that the problem is on Mathematica side. I think that NIntegrate gives correct results but probably your problem formulation is wrong somewhere. But if you just try to reproduce results from published paper why have not you given direct link to that paper? It would allow people to give much more adequate help. — Alexey Popkov, Dec 26 '13 at 13:07
i'm not exactly reproducing journal results but a simulation, and i know for sure that a reflection peak has to result in a ep2 (imaginary) peak. i tried your case for another simulation for the case of lorentzian ep2 to ep1 but failed which you can try to take a look in the update of my answer. — user11251, Dec 26 '13 at 14:54
I think that original question about NIntegrate is answered. What we discuss now is out of scope of the original question formulation. The reason why you get artifacts using Plot is that NIntegrate fails to give correct value of the integral for some points on which Plot calls it. — Alexey Popkov, Dec 28 '13 at 13:20
This gives plot without artifacts and much faster than your original approach: ep2[w_] := ep2[w] = 1 + 2/Pi NIntegrate[(a f[a])/(a^2 - w^2), {a, 0, w, 10}, Method -> {"PrincipalValue", "SingularPointIntegrationRadius" -> .01, Method -> {"InterpolationPointsSubdivision", "MaxSubregions" -> 10^9}}] // Quiet; Plot[ep2[w], {w, 0, 10}, AxesOrigin -> {0, 0}, PlotRange -> {{0, 10}, {-90, 90}}] — Alexey Popkov, Dec 28 '13 at 13:31
Hello Alexey, I have new questions regarding numerical integration. Not sure if you will get the notification through an edit so I'm replying here. Thanks in advanced. — user11251, Jan 06 '14 at 06:52
Your "column table method" is not a method at all. With Table I get exactly the same output for tetha[0.1] as the above: -0.08929167468426512` (the second line of the output). I feel that you do not really understand what are you doing and what you expect to get with Mathematica. Apart of this you disregard rules of this site: you should ask a question and then if one give you an answer you should decide whether the question is answered and then accept the answer if it answers the original question. Extended discussions in answers and comments are not allowed. — Alexey Popkov, Jan 06 '14 at 07:07

Kramers Kronig Relation for Phase and Complex Reflectivity

2 Answers2