Checking whether a number can be composed from the cube of its digit

Question

How to check whether or not the sum of the cube of each digit of a number is equal to the number itself?

In the following code, I tried to return the number in question whenever it matches the condition.

In[191]:= Func[x_]:=If[Total[Map[#^3& ,IntegerDigits[x]]]==x,x,0];
Func[300]

Out[192]= 300

Apparently the checking seems to be wrongly done. What caused this issue? How to fix it?

Have you reset the Kernel before? Maybe there is some old definition for Func. p.s. you don't have to Map in such cases: Total[IntegerDigits[300]^3] will do too. — Kuba, Dec 30 '13 at 15:40
@cormullion: Oh my ghost, I forgot to kill the kernel first. — kiss my armpit, Dec 30 '13 at 15:40

score 7 · Accepted Answer · edited Apr 13 '17 at 12:55

We would like to find all integers x satisfying the following equation Total[ IntegerDigits[x]^3] == x (we don't have to map #^3& since Power is Listable).

Warning: Flexibility and polymorphism of Mathematica notation is restricted by Operator Precedence (see also When is f@g not the same as f[g]?). It appears to be the case here. One could suspect this was the problem defining Func initially.

f[x_] := Total[ IntegerDigits[x]^3] == x

however we might get incorrect results using this definition Total @ IntegerDigits @ x^3 == x while this one works fine Total[ IntegerDigits @ x^3] == x.

Select[ Range[0, 10^5], f @ # &]

{0, 1, 153, 370, 371, 407}

One can easily observe that we don't have to search for such integers anymore since Total[ IntegerDigits[x]^3] increases in a polynomial rate with the exponent in Range while x increases in an exponential rate and

Total[ IntegerDigits[99999]^3] < 10^5

True

Thus the above are all integers satisfying Total[ IntegerDigits[x]^3] == x.

Edit

Out of curiosity I have found how the solutions depend on the exponent. Defining:

f[x_, k_] := Total[ IntegerDigits[x]^k] == x

immediately we find with Select[ Range[ 0, 10^4], f[#, 2]&] that for k == 2 there are no solutions (besides 0 and 1).

ListPlot[ 
  Append[ 
    Table[ Log @ Total[ IntegerDigits[10^k - 1]^m], {m, 3, 9}, {k, 15}], 
    Table[ Log[ 10^(k - 1)], {k, 15}]], AxesOrigin -> {1, 0}, 
  PlotMarkers -> {Automatic, Medium}, PlotRange -> All, Joined -> True,
  PlotStyle -> Thick, PlotLegends -> Range[3, 9]]

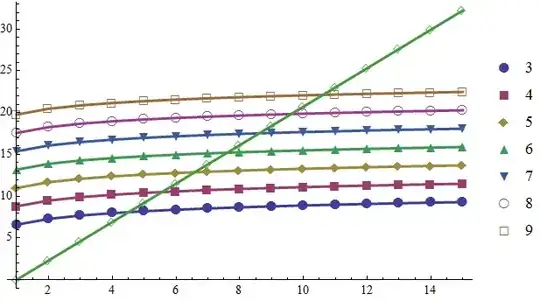
enter image description here

With this plot it appears to be easier to estimate appropriate range of search space. We've got:

Select[ Range[10^6], f[#, 4]&]

{ 1, 1634, 8208, 9474}

Select[ Range[10^7], f[#, 5]&]

{ 1, 4150, 4151, 54748, 92727, 93084, 194979}

Select[ Range[5 10^7], f[#, 6]&]

{ 1, 548834}

score 2 · Answer 2 · answered Dec 30 '13 at 15:47

2

It works as Artes showed, but here's, not faster but why not, another approach:

func = (1 - Unitize[Norm[IntegerDigits[#], 3]^3 - #]) # &

for clarification, see the documentation for Norm and it's second argument.

answered Dec 30 '13 at 15:47

Kuba

136,707
13
279
740

Checking whether a number can be composed from the cube of its digit

2 Answers2