2

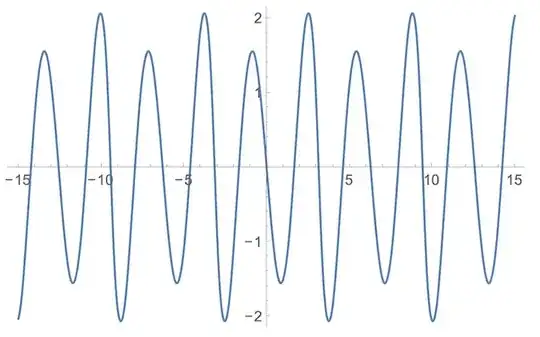
I want to plot this: $\displaystyle\sum_{n=-{10}\atop n\ne \pm 1}^{10} \dfrac {4i(-1)^{n}n}{(n^2 - 1)^2}e^{inx}$

but have no idea how I can exclude the cases for when $ n = \pm 1 $. I don't wish to split up the summation into two parts either.

Thanks.

Tom
  • 73
  • 4

2 Answers2

4

I actually couldn't find a question on exclusion of summation indices. Let me know if I missed it.

f[x_] = 
Sum[(4 I (-1)^n n)/(1 - n^2)^2 Exp[I n x], {n, Complement[Range[-10, 10], {-1, 1}]}] //  
FullSimplify;

or even more proper

f[x_] = Sum[(4 I (-1)^n n)/(1 - n^2)^2 Exp[I n x], 
        {n, DeleteCases[Range[-10, 10], Alternatives @@ {-1, 1}]}] // FullSimplify;

f[x] // TraditionalForm

enter image description here

Plot[f[x], {x, -15, 15}]

enter image description here

Community
  • 1
Vitaliy Kaurov
  • 73,078
  • 9
  • 204
  • 355
1

Maybe the simplest approach

Sum[If[n == -1 || n == 1, 0, (4 I (-1)^n n)/(1 - n^2)^2 Exp[I n x]], {n, -10, 10}]
ybeltukov
  • 43,673
  • 5
  • 108
  • 212