Possibility of evaluating the expression within a NestList at each iteration?

Question

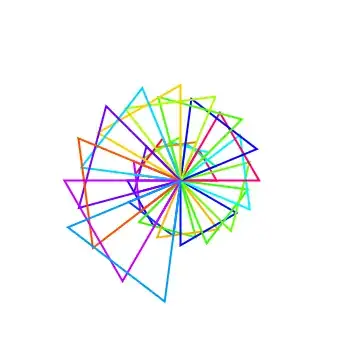
I want to rotate iteratively a triangle about the same point, increasing for each iteration the length of its side in the same proportion and change the color of its sides.
I came up with the solution below:

triangle[x_] := 
Line[ {{0, 0}, {1 + x, 0}, {(1 + x)/2, (Sqrt[3] (1 + x)/2)}, {0, 0}}]
randomcolor[] := Apply[RGBColor, RandomReal[1, {3}]]
Show[Array[Graphics[Rotate[{Thick, randomcolor[], triangle[#]}, # (Pi/5), {0, 
  0}]] &, 3]]       (* a simple output *)
Show[Array[Graphics[Rotate[{Thick, randomcolor[], triangle[#]}, # (Pi/9), {0, 
  0}]] &, 180]]   (* more elaborated *)

There are certainly other and better ways to achieve this result. However my first attempt for my solution was to use NestList which I felt to be more suitable but could not proceed further than this line:

rot[gr_] := Rotate[gr, Pi/16, {0, 0}]
Graphics[{NestList[rot, triangle[#], #]}] & [2]

The same figure is repeated which is as expected there but is there any way at the start of each iteration to re-evaluate the value of the function triangle[#] with the current value of the Nestlist iterator?

Answer 1

If you need an iterator you can do something like:

i=0; and put somewhere i++ but it will not be straightforward with functions you have. You can use FoldList too, e.g:

Graphics @ Rest @ FoldList[
                    Rotate[{Hue[#2/10], triangle[#2]}, #2 Pi/16, {0, 0}] &,
                    1, 
                    Range[2, 10]]

Or another approach, with NestList but also with Scale since you want the ratio to be constant:

tri = Line[{{0, 0}, {1, 0}, {.5, Sqrt[3]/2}, {0, 0}}]
p0 = {0, 0};
ratio = 1.05;
angle = Pi/8;
i = 25;

Graphics[
 NestList[
  {Hue@RandomReal[], Rotate[Scale[#[[2]], ratio, p0], angle, p0]} &,
  {Hue@RandomReal[], tri},
  i]
, PlotRange -> 5, BaseStyle -> Thick]