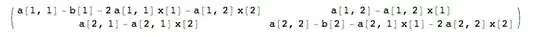Symbolic Jacobian computation

Question

I have an equation for which I would like to compute the Jacobian symbolically.

$$f(x)=Ax-diag(x)(Ax+b)$$, where $x\in \mathbb{R}^n$, $A\in \mathbb{R}^{n\times n}$ and $b\in \mathbb{R}^n$.

I am new to Mathematica, and I have seen this relevant question, but I am not aware of how to automatically ensure Mathematica recognises the different dimensions. Can someone help me how to code that in Mathematica?

Just to clarify, are $n$, $A$, and $b$ unknown symbolic constants? — Michael E2, Jan 16 '14 at 12:33
You posted another question, but formulated the problem differently. I assume it is the same problem in both questions? — Wojciech, Jan 16 '14 at 12:38
@Wojciech: Same equation, but I need the zeros in the other question. Here it is the Jacobian. — Bravo, Jan 16 '14 at 12:39

score 4 · Answer 1 · answered Jan 16 '14 at 13:32

4

Define the elements and the function f:

n=2;
aMat = Array[a, {n, n}];
xVec = Array[x, n];
bVec = Array[b, n];
f[xVec_] := aMat.xVec - DiagonalMatrix[xVec].(aMat.xVec + bVec);

The Jacobian is:

D[f[xVec], {xVec}]
MatrixForm[%]

enter image description here

It seems to work fine for fairly large values of n.

answered Jan 16 '14 at 13:32

bill s

68,936
4
101
191

just to note the JacobianMatrix defined in the linked answer works fine with these defs JacobianMatrix[f[xVec], xVec] - now what would be really nice is to do this symbolically (i.e. w/o pre defining the matrix terms) – george2079 Jan 16 '14 at 15:40

Symbolic Jacobian computation

1 Answers1