Generate list of strings from a list of assigned variables

Question

How do I generate a list of strings from a list of assigned variables?

E.g. convert

var1 = 10;
var2 = 11;
var3 = 17;
var4 = 5;

compvar = {var1, var2, var3, var4}; (*all variables assigned*)

into

compvarstr = {"var1", "var2", "var3", "var4"};

Using ToString obviously converts the variables assignments into strings e.g.

compvarstr = ToString[#] & /@ compvar

gives,

 {"10", "11", "17", "5"}

I'm after the unassigned variable names as strings e.g.

 {"var1", "var2", "var3", "var4"};

Apologies if this is a duplicate - I had a bit of a look and nothing seemed to answer it.

@Nasser - please review my edit. I hope the question is clearer now. — geordie, Jan 18 '14 at 02:51
I see now after your edits. But what you are asking for can't be done as is. Once you make an assignment, compvar becomes {10, 11, 17, 5}, becuase M has evaluated all those variables to their values. Only way, is not to make the assignment to the valuates, but using replacement rule. I'll post an example — Nasser, Jan 18 '14 at 02:53

score 9 · Answer 1 · answered Jan 18 '14 at 05:34

Here's a way:

var1 = 10;
var2 = 11;
var3 = 17;
var4 = 5;
compvar := {var1, var2, var3, var4}
compvar; (*all variables assigned*)

ClearAll[f];
SetAttributes[f, {HoldAll}];
f[x_, y__] := Flatten@{f[x], f[y]}
f[x_] := SymbolName@Unevaluated@x

OwnValues[compvar] /. {HoldPattern[y_] :> {x__}} :> f[x]

(*
 {"var1", "var2", "var3", "var4"}
*)

score 7 · Accepted Answer · edited Apr 13 '17 at 12:55

You must introduce some form of holding in you definition of compvar as otherwise, assuming it is defined after var1, var2, etc., there is no information to retrieve:

var1 = 10;
var2 = 11;
var3 = 17;
var4 = 5;

compvar = {var1, var2, var3, var4};

Definition[compvar]

compvar = {10, 11, 17, 5}

You could use Hold but then you would need to ReleaseHold (or similar) every time you used compvar. Instead I suggest you use SetDelayed and then recover the definition using my step function from:

How do I evaluate only one step of an expression?

It returns an expression wrapped in HoldForm:

compvar := {var1, var2, var3, var4};

step[compvar] // InputForm

HoldForm[{var1, var2, var3, var4}]

To convert to a list of strings:

Cases[step[compvar], s_Symbol :> SymbolName @ Unevaluated @ s, {2}]

{"var1", "var2", "var3", "var4"}

Or:

StringSplit[ToString @ step[compvar], ("{" | "," | " " | "}") ..]

{"var1", "var2", "var3", "var4"}

The first method will return Symbols (as strings) only while the second will convert other expressions as well.

Incidentally if you do not need to store your Symbols in a List you could use a more direct form:

compHeld = Hold[var1, var2, var3, var4];

List @@ SymbolName /@ Unevaluated /@ compHeld

{"var1", "var2", "var3", "var4"}

@geordie You're welcome, and thanks for the Accept. – Mr.Wizard Jul 27 '14 at 12:17 — Mr.Wizard, Jul 27 '14 at 12:17

score 5 · Answer 3 · answered Jan 18 '14 at 03:01

5

one way is to make a replacement rule seperately and use that.

Clear[var1, var2, var3, var4];
vars = {var1, var2, var3, var4};
values = {var1 -> 10, var2 -> 11, var3 -> 17, var4 -> 5};
compvar = vars /. values

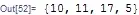
Mathematica graphics

compvarstr = ToString[#] & /@ vars
FullForm[compvarstr]

Mathematica graphics

Otherwise, the way you had it:

 var1 = 10; var2 = 11; var3 = 17; var4 = 5;
 compvar = {var1, var2, var3, var4}; (*all variables assigned*)

Now the var1 name itself is replaced by 10 right away by the evaluator. Hence compvar will always be {10, 11, 17, 5} and the name of the variables is not known inside compvar since their value is used.

answered Jan 18 '14 at 03:01

Nasser

143,286
11
154
359

This wont work for my case (setting up the rules each time will be a fiddle) but it has made me realise that going the other way is easy e.g. compvar = ToExpression[compvarstr]. Many thanks! – geordie Jan 18 '14 at 03:10
@geordie if that works for you then good. But I think writing values = {var1 -> 10, var2 -> 11, var3 -> 17, var4 -> 5}; is not more a problem than writing var1 = 10; var2 = 11; var3 = 17; var4 = 5; and using replacement rule is more flexible in many other ways and for many other uses as well. But again, whatever works for you ;) – Nasser Jan 18 '14 at 03:13
Agreed, however, in my full code "var1" through "var4" are nested lists and have names like "vh88exp1", "vh88sswl", "bpqm10", etc... So it is quite easy for me to write out their names as a list of strings. Thanks again. – geordie Jan 18 '14 at 03:24

score 5 · Answer 4 · answered Dec 17 '14 at 06:57

Better late the never, right? I created this answer while thinking about one of recent questions that was a duplicate of this one.

I kind of like this way, it is compact and without #&@ :)

ClearAll[VNL];
SetAttributes[VNL, HoldFirst];

VNL[list_] :=   Thread[
                       Hold[list] /. OwnValues[list]
                       ] /.    Hold[s_] :> (SymbolName[Unevaluated[s]])

Let's borrow belisarius' variables :)

var1 = 10;
var2 = 11;
var3 = 17;
var4 = 5;
compvar := {var1, var2, var3, var4}

VNL[ compvar ]

  {"var1", "var2", "var3", "var4"}

score 4 · Answer 5 · edited Apr 13 '17 at 12:55

Here is another alternative, in which the values of the variables are temporarily cleared using Block and an injector pattern.

ClearAll[getSymbolNames];
SetAttributes[getSymbolNames, HoldAll];
getSymbolNames[list_Symbol] := 
 Hold[list] /. OwnValues[list] /. 
  Hold[{vars__Symbol}] :> Block[{vars}, SymbolName /@ {vars}]

With some planning one might initialized the list of variables before the values to var1 etc. are assigned; otherwise, use SetDelayed as in the other answers.

Clear[var1, var2, var3, var4];
compvar0 = {var1, var2, var3, var4};

var1 = 10;
var2 = 11;
var3 = 17;
var4 = 5;

compvar := {var1, var2, var3, var4};

getSymbolNames[compvar0]
(*  {"var1", "var2", "var3", "var4"}  *)

getSymbolNames[compvar]
(*  {"var1", "var2", "var3", "var4"}  *)

score 1 · Answer 6 · answered Nov 21 '17 at 03:24

Redefine your data in an associative way

data=<|
"var1"->10,
"var2"->11,
"var3"->17,
"var4"->5
|>

because it looks like you are simply looking for the Keys and the Values of your data

compvar = Values@data
compvarstr = Keys@data

{10, 11, 17, 5}

{"var1", "var2", "var3", "var4"}

Generate list of strings from a list of assigned variables

6 Answers6

Linked

Related