How do I fill the area from 0 to pi in my Sine wave and in the process get the area value?

Question

I am new to Mathematica and I tried searching the docs but no specific examples there.

This is what I have achieved so far, returns an error, probably wrong syntax.

Plot[ Sin[x], {x, 0, 2 Pi}, Filling -> Range {x, 0, Pi}]

Try Plot[{If[0 < x < Pi, Sin[x]], Sin[x]}, {x, 0, 2 Pi}, Filling -> {1 -> Axis}] For area take a look at Integrate. — Kuba, Jan 20 '14 at 14:53
Thanks @Kuba, and bills: I need a single value for the area. Anyway, can Mathematica could do this automatically, with a special function that allows me to integrate and in the process, it does the shade. — Ali Gajani, Jan 20 '14 at 15:03
What do you mean by "in the process"? Do you want an animated graphics with shading increasing along time and some text indicating the area of current shaded region? — Silvia, Jan 27 '14 at 20:27
To the close voters: how is this easily found in the documentation? The OP did not merely ask how to compute the area under the curve, but how to do it "in the process" of plotting. I believe my answer describes this, and I cannot recall seeing that in the documentation. — Mr.Wizard, Jan 28 '14 at 05:58

score 6 · Answer 1 · answered Jan 20 '14 at 15:39

6

No, there is no "special function that allows me to integrate and in the process, it does the shade", but you can shade the area and plot the points used in the integration. For example:

f[x_?NumericQ] := Sow[{x, Sin[x]}][[2]]
{#[[1]], Plot[f@x, {x, 0, Pi}, Epilog -> Point@#[[2]], 
              Filling -> Axis]} &@Reap@NIntegrate[f[x], {x, 0, Pi}]

Mathematica graphics

answered Jan 20 '14 at 15:39

Dr. belisarius

115,881
13
203
453

Thanks, but getting an error. SetDelayed::write: Tag InterpolatingFunction in <<1>>[x_?NumericQ] is Protected. >> and InterpolatingFunction::dmval: "Input value {0.0000641782} lies outside the range of data in the interpolating function. Extrapolation will be used." – Ali Gajani Jan 20 '14 at 15:42
@AliGajani Restart your Mathematica session and try again – Dr. belisarius Jan 20 '14 at 15:43
Same @belisarius :( Anyway, how come I use NIntegrate on sinx and it won't reveal -cos x but some random pile of numbers. I'd love some guidance in this regard as well. Thank you. – Ali Gajani Jan 20 '14 at 15:47
2

Belisaius code works fine. Copy/paste it and choose Evaluation->Quit Kernel->Local to remove previous definitions (that are causing the errors). Use Integrate instead of NIntegrate if you want it done symbolically rather than numerically. – bill s Jan 20 '14 at 16:01
Thanks, that works Bill s. Also, I did "Integrate Sin x" and it returns 1/2 Integrate Sin x^2 as the output, weird. – Ali Gajani Jan 20 '14 at 16:11
You need to use correct syntax: Integrate[Sin[x], {x, 0, Pi}] – bill s Jan 20 '14 at 16:15
I get that, I am talking about the symbolic integration of sin x which should return -cos x + c , I hope you understand. – Ali Gajani Jan 20 '14 at 16:17
1

@AliGajani, I think you are looking for the indefinite integral Integrate[Sin[x], x]. You may benefit from reading the documentation for Integrate, perhaps start here: How to Do an Integral – Simon Woods Jan 20 '14 at 17:08
Thanks, I figured it out just like 15 mins before your reply, Thanks again. :) – Ali Gajani Jan 20 '14 at 17:10

score 5 · Answer 2 · edited Jan 20 '14 at 17:55

5

I don't really understand the question but you can try this:

Manipulate[Plot[{Sin[x], Sin[x] Boole[x < y]}, {x, 0, Pi}, 
    Filling -> 2 -> Axis, Frame -> True, 
    ImageSize -> 500, Epilog -> Inset[NIntegrate[Sin[x], 
      {x, 0, y}], {y, 1/2 Sin[y]}, {Right, Center}]], {y, 0, Pi}
]

edited Jan 20 '14 at 17:55

Stefan

5,347
25
32

answered Jan 20 '14 at 17:44

Grisha Kirilin

641
4
9

score 5 · Answer 3 · edited Apr 13 '17 at 12:56

Taking the question at face value: you can calculate the area of the fill from the Graphics object that is generated by Plot, specifically the Polygon expression.

I will use this fill method and my old polyarea code.

The plot:

gr = Plot[{If[x < Pi, Sin[x]], Sin[x]}, {x, 0, 2 Pi}, Filling -> {1 -> Axis}]

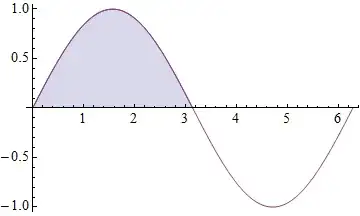
enter image description here

The area:

polyarea = 
  Compile[{{v, _Real, 2}}, 
   Block[{x, y}, {x, y} = Transpose@v; 
    Abs[x.RotateLeft@y - RotateLeft@x.y]/2]];

Cases[Normal @ gr, Polygon[a_?ArrayQ] :> polyarea[a], {-4}]

{1.99894}

Normal is needed to convert the GraphicsComplex data into plain coordinate data.

Additional Plot precision will yield additional numeric precision:

gr = Plot[{If[x < Pi, Sin[x]], Sin[x]}, {x, 0, 2 Pi},
      Filling -> {1 -> Axis}, 
      Method -> {MaxBend -> 0.5}];

Cases[Normal @ gr, Polygon[a_?ArrayQ] :> polyarea[a], {-4}]

{1.99998}

For a function that crosses the axis you will need to account for the sign. For example:

Plot[Re[Zeta[1/2 + I t]], {t, -7, 20}, Filling -> Axis, Method -> {MaxBend -> 0.2}]

Cases[Normal @ %, Polygon[a_?ArrayQ] :> Sign@Last@Mean@a * polyarea@a, {-4}]

Total @ %

enter image description here

{-0.00312878, -1.15988, 7.2798, 3.74814, 11.4189}
21.2838

Confirmation of the area calculated with NIntegrate:

NIntegrate[Re[Zeta[1/2 + I t]], {t, -7, 20}]

21.2838

How do I fill the area from 0 to pi in my Sine wave and in the process get the area value?

3 Answers3