How to "ReplaceAll" using a set of conditional expressions instead of a list of rules

Question

Suppose that I have two linear functions

f[x_] := f0 + f1 x
g[x_] := g0 + g1 x

and a (possibly rather complicated) set of conditional expressions, obtained through Reduce. For example, we might have something like this:

conditions = (f0 == f1 && g0 == 0) || (f0 == g1 && g0 == f1)

What I would like to do is write something like

{f[x],g[x]} /. conditions

and receive as output the set of pairs of $f$ and $g$ adhering to that formula. In this case we'd have

{{a + ax, bx}, {a + bx, b + ax}}

(or maybe {{f0 + f0x, g1x}, {f0 + f1x, f1 + f0x}} to stick with original variable names).

How can I do this?

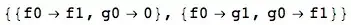
@Mr.Wizard I get the conditions through Reduceing a system of equations in $g_0,g_1,f_0,f_1$ and then FullSimplifying, so these should be solutions. I'm really just trying to transform the coefficient logic into polynomial logic. — Alexander Gruber, Jan 27 '14 at 08:37
According to the documentation for Reduce, this is how: {f[x], g[x]} /. {ToRules@conditions}. The only issue is adjusting the variables in Reduce to get them in the order you desire. (It's unclear whether you want f0 replaced by f1 or vice versa, or sometimes both.) — Michael E2, Jan 27 '14 at 11:30
As suggested by MichaelE2 {f[x], g[x]} /. {ToRules @ conditions} is what you need. See e.g. How to get intersection values from a parametric graph? where Solve couldn't provide solutions so we had used ToRules @ Reduce[...]. Another useful method you might find here: Simplifying expressions with square roots. — Artes, Jan 27 '14 at 13:29

TransferOrbit · Answer 1 · 2014-01-27T10:27:03.933

4

First convert your conditions to a list of Rules

myrules = Apply[List, conditions /. {Equal -> Rule}, {0, 1}]

which gives

enter image description here

ReplaceAll[{f[x], g[x]}, #] & /@ myrules

which produces

enter image description here

edited Jan 27 '14 at 10:27

answered Jan 27 '14 at 09:02

TransferOrbit

score 2 · Answer 2 · answered Jan 27 '14 at 09:33

2

Assuming[#, Simplify[{f[x], g[x]}]] & /@ List @@ conditions

{{f1 (1 + x), g1 x}, {g1 + g0 x, g0 + g1 x}}

Which, technically but with switched constants, is what is desired.

answered Jan 27 '14 at 09:33

Kuba

2 Answers2