4

I want to fit experimental data by the H-N model. Here is the H-N model: $$\text{EHN}(T)\text{=}\text{E$\infty $}+\frac{\text{E0}-\text{E$\infty $}}{\left(1+\left(i \omega\tau(T_g)10^{-\frac{\text{C1} (T-\text{Tg})}{\text{C2}+(T-\text{Tg})}}\right)^{\alpha }\right)^{\beta }}$$

Here is my data and code.

   dataRe={{135., 2286.88}, {136., 1889.46}, {137., 1567.42}, {138., 
          1294.73}, {139., 1081.55}, {140., 902.773}, {141., 761.623}, {142., 
          643.534}, {143., 550.366}, {144., 470.925}, {145., 405.269}, {146., 
          348.847}, {147., 303.248}, {148., 263.789}, {149., 230.926}, {150., 
          202.368}, {151., 178.676}, {152., 158.557}, {153., 142.725}, {154., 
          129.218}, {155., 118.192}, {156., 108.735}, {157., 101.272}, {158., 
          94.8359}, {159., 89.3741}, {160., 84.4597}, {161., 80.1335}, {162., 
          76.1632}, {163., 72.6128}, {164., 69.2969}, {165., 66.227}, {166., 
          63.3502}, {167., 60.7664}, {168., 58.3432}, {169., 56.0645}, {170., 
          53.8886}, {171., 51.8571}, {172., 49.9009}, {173., 48.014}, {174., 
          46.1953}, {175., 44.4969}, {176., 42.8668}, {177., 41.3076}, {178., 
          39.7966}, {179., 38.3511}, {180., 36.9621}, {181., 35.6673}, {182., 
          34.4443}, {183., 33.3239}, {184., 32.2584}, {185., 31.245}, {186., 
          30.2813}, {187., 29.4031}, {188., 28.5708}, {189., 27.781}, {190., 
          27.0241}, {191., 26.3191}, {192., 25.6392}, {193., 24.975}, {194., 
          24.3329}, {195., 23.7381}, {196., 23.1738}, {197., 22.6451}, {198., 
          22.1308}, {199., 21.6239}, {200., 21.1439}, {201., 20.7245}, {202., 
          20.3002}, {203., 19.8216}, {204., 19.3485}, {205., 18.9218}, {206., 
          18.5166}, {207., 18.1276}, {208., 17.7492}, {209., 17.3845}, {210., 
          17.0318}, {211., 16.6938}, {212., 16.3641}, {213., 16.0424}, {214., 
          15.7233}, {215., 15.4063}, {216., 15.0967}, {217., 14.8008}, {218., 
          14.5269}, {219., 14.2817}, {220., 14.0376}, {221., 13.7849}, {222., 
          13.5334}, {223., 13.288}, {224., 13.0538}, {225., 12.831}, {226., 
          12.6145}, {227., 12.4025}, {228., 12.1932}, {229., 11.9889}, {230., 
          11.8003}, {231., 11.622}, {232., 11.442}, {233., 11.2606}, {234., 
          11.0808}, {235., 10.9046}, {236., 10.7371}, {237., 10.577}, {238., 
          10.4275}, {239., 10.2802}, {240., 10.1313}, {241., 9.98528}, {242., 
          9.84445}, {243., 9.70511}, {244., 9.56583}, {245., 9.42439}, {246., 
          9.28424}, {247., 9.16163}, {248., 9.05307}, {249., 8.94078}, {250., 
          8.82361}, {251., 8.70563}, {252., 8.58908}, {253., 8.47813}, {254., 
          8.37066}, {255., 8.26599}, {256., 8.16324}, {257., 8.06268}, {258., 
          7.9627}, {259., 7.86389}, {260., 7.77106}, {261., 7.68272}, {262., 
          7.59522}, {263., 7.50776}, {264., 7.4199}, {265., 7.33254}, {266., 
          7.24746}, {267., 7.16453}, {268., 7.0849}, {269., 7.00582}, {270., 
          6.92552}, {271., 6.84306}, {272., 6.76014}, {273., 6.68684}, {274., 
          6.62505}, {275., 6.56069}, {276., 6.4861}, {277., 6.4139}, {278., 
          6.34826}, {279., 6.28453}, {280., 6.2223}, {281., 6.16394}, {282., 
          6.10795}, {283., 6.04993}, {284., 5.99424}, {285., 5.94735}, {286., 
          5.90123}, {287., 5.84622}, {288., 5.78872}, {289., 5.74026}, {290., 
          5.69521}, {291., 5.65082}, {292., 5.60682}, {293., 5.56378}, {294., 
          5.52176}, {295., 5.48153}, {296., 5.44198}, {297., 5.40113}, {298., 
          5.36029}, {299., 5.32389}, {300., 5.29061}, {301., 5.25599}, {302., 
          5.22026}, {303., 5.18636}, {304., 5.15429}, {305., 5.12238}, {306., 
          5.09002}, {307., 5.05626}, {308., 5.0215}, {309., 4.9884}, {310., 
          4.95724}, {311., 4.9259}, {312., 4.89414}, {313., 4.86346}, {314., 
          4.83431}, {315., 4.80636}, {316., 4.77938}, {317., 4.75121}, {318., 
          4.72102}, {319., 4.69132}, {320., 4.66365}, {321., 4.63793}, {322., 
          4.61535}, {323., 4.5939}, {324., 4.57255}, {325., 4.55129}, {326., 
          4.53031}, {327., 4.50947}, {328., 4.48862}, {329., 4.46747}, {330., 
          4.44536}, {331., 4.42347}, {332., 4.40477}, {333., 4.3878}, {334., 
          4.36821}};
    dataIm={{135., 887.339}, {136., 797.248}, {137., 701.968}, {138., 
      608.569}, {139., 523.492}, {140., 445.966}, {141., 379.817}, {142., 
      322.098}, {143., 274.838}, {144., 234.408}, {145., 201.682}, {146., 
      173.669}, {147., 150.826}, {148., 130.956}, {149., 114.338}, {150., 
      99.8744}, {151., 87.8489}, {152., 77.4709}, {153., 69.0043}, {154., 
      61.7297}, {155., 55.8849}, {156., 50.8427}, {157., 46.6994}, {158., 
      43.0493}, {159., 39.9282}, {160., 37.1165}, {161., 34.6505}, {162., 
      32.3913}, {163., 30.3725}, {164., 28.5008}, {165., 26.8072}, {166., 
      25.2321}, {167., 23.8052}, {168., 22.4737}, {169., 21.258}, {170., 
      20.1175}, {171., 19.0709}, {172., 18.0847}, {173., 17.1751}, {174., 
      16.3173}, {175., 15.5259}, {176., 14.7758}, {177., 14.076}, {178., 
      13.4098}, {179., 12.7869}, {180., 12.1926}, {181., 11.6359}, {182., 
      11.1054}, {183., 10.6106}, {184., 10.141}, {185., 9.7062}, {186., 
      9.29656}, {187., 8.922}, {188., 8.57166}, {189., 8.25434}, {190., 
      7.95882}, {191., 7.69154}, {192., 7.44172}, {193., 7.21152}, {194., 
      6.99187}, {195., 6.78149}, {196., 6.57857}, {197., 6.38792}, {198., 
      6.20788}, {199., 6.0449}, {200., 5.89388}, {201., 5.758}, {202., 
      5.62656}, {203., 5.49434}, {204., 5.36374}, {205., 5.23765}, {206., 
      5.11653}, {207., 5.00326}, {208., 4.89584}, {209., 4.79588}, {210., 
      4.70075}, {211., 4.61033}, {212., 4.52086}, {213., 4.43049}, {214., 
      4.33572}, {215., 4.23482}, {216., 4.13749}, {217., 4.04895}, {218., 
      3.96654}, {219., 3.89063}, {220., 3.81765}, {221., 3.74721}, {222., 
      3.67986}, {223., 3.61563}, {224., 3.55026}, {225., 3.48314}, {226., 
      3.41624}, {227., 3.34984}, {228., 3.28314}, {229., 3.2159}, {230., 
      3.14784}, {231., 3.08}, {232., 3.01543}, {233., 2.95542}, {234., 
      2.90456}, {235., 2.85808}, {236., 2.81372}, {237., 2.76943}, {238., 
      2.72368}, {239., 2.67735}, {240., 2.6309}, {241., 2.58498}, {242., 
      2.54007}, {243., 2.49639}, {244., 2.45405}, {245., 2.41249}, {246., 
      2.37127}, {247., 2.32927}, {248., 2.28662}, {249., 2.24441}, {250., 
      2.20277}, {251., 2.16184}, {252., 2.12168}, {253., 2.0829}, {254., 
      2.04515}, {255., 2.00862}, {256., 1.97252}, {257., 1.93656}, {258., 
      1.90105}, {259., 1.8665}, {260., 1.83418}, {261., 1.80359}, {262., 
      1.77372}, {263., 1.74444}, {264., 1.71617}, {265., 1.68854}, {266., 
      1.66149}, {267., 1.63461}, {268., 1.60756}, {269., 1.5805}, {270., 
      1.55363}, {271., 1.52752}, {272., 1.50251}, {273., 1.47878}, {274., 
      1.45619}, {275., 1.43259}, {276., 1.40649}, {277., 1.38075}, {278., 
      1.35628}, {279., 1.33193}, {280., 1.30753}, {281., 1.28371}, {282., 
      1.26006}, {283., 1.23519}, {284., 1.21085}, {285., 1.18961}, {286., 
      1.16996}, {287., 1.15244}, {288., 1.13717}, {289., 1.12452}, {290., 
      1.11253}, {291., 1.10009}, {292., 1.08708}, {293., 1.07289}, {294., 
      1.05803}, {295., 1.04329}, {296., 1.02881}, {297., 1.01485}, {298., 
      1.00133}, {299., 0.98825}, {300., 0.97555}, {301., 0.96326}, {302., 
      0.95127}, {303., 0.93939}, {304., 0.92759}, {305., 0.91595}, {306., 
      0.90446}, {307., 0.89313}, {308., 0.88195}, {309., 0.87097}, {310., 
      0.86024}, {311., 0.84998}, {312., 0.84021}, {313., 0.83063}, {314., 
      0.82119}, {315., 0.81193}, {316., 0.80287}, {317., 0.79377}, {318., 
      0.78453}, {319., 0.77542}, {320., 0.76659}, {321., 0.75783}, {322., 
      0.74902}, {323., 0.74036}, {324., 0.73211}, {325., 0.72417}, {326., 
      0.71666}, {327., 0.70927}, {328., 0.70162}, {329., 0.69383}, {330., 
      0.68607}, {331., 0.67845}, {332., 0.67127}, {333., 0.66448}, {334., 
      0.65796}};

EHN[T_] := E\[Infinity] + (E0 - E\[Infinity])/(1 + (I \[Omega] 10^(-((C1 (T - T0))/(C2 + (T - T0)))))^\[Alpha])^\[Beta];
     fitRe=FindFit[dataRe,Re[EHN[T]],{{\[Alpha], 0.2}, {\[Beta], 0.6}, {E0, 4}, {E\[Infinity], 8000}, {C1, 
          17}, {C2, 50}, {\[Omega], 10}}, {T}}];
    fitIm=FindFit[dataIm,Im[EHN[T]],{{\[Alpha], 0.2}, {\[Beta], 0.6}, {E0, 4}, {E\[Infinity], 8000}, {C1, 
          17}, {C2, 50}, {\[Omega], 10}}, {T}}];
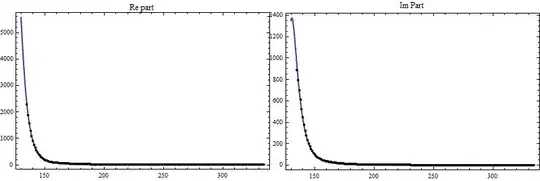
    Show[ListPlot[dataRe, PlotStyle -> Red], Plot[Re[EHN[T]] /. {fitRe}, {T, 1, 200}]]
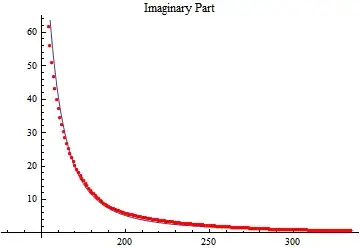
    Show[ListPlot[dataIm, PlotStyle -> Orange], Plot[Im[EHN[T]] /. {fitIm}, {T, 1, 250}]]

However,I cannot fit the Real part and the Imaginary part well.Here is one of my fitted picture: enter image description here

Is there any method,which I can fit both the Re and Im part. Thanks.

Yuuhsing Tuan
  • 75
  • 5

2 Answers2

5

The model you are using in your code is missing a T0 which is shown in your question. I don't know why you would have arbitrarily dropped the parameter, but I have answered this question assuming that you know what you are doing. Using the approach described here you can model the Real and Imaginary parts simultaneously with using NonlinearModelfit:

model[T_, E∞_, E0_, ω_, C1_, T0_, C2_, α_, β_][part_] := Module[{f},
   f = If[part == 1, Re, Im];
   f[E∞ + (E0 - E∞)/(1 + 
     (I ω  10^(-((C1 (T - T0))/(C2 + (T - T0)))))^α)^β]];

data = Join[ {#[[1]], 1, #[[2]]} & /@ dataRe, {#[[1]], 0, #[[2]]} & /@
     dataIm];

nlm = NonlinearModelFit[data, 
  model[T, E∞, E0, ω, C1, T0, C2, α, β][
   part], {{α, 0.2}, {β, 0.6}, {E0, 4}, {E∞, 
    8000}, {C1, 17}, {C2, 50}, {ω, 10}, {T0, 110}}, {T, part}]

nlm["BestFitParameters"]
(* {α -> 0.325145, β -> 4.0862, E0 -> 7.3715, E∞ -> 6021.86, C1 -> 16.1477, 
    C2 -> 26.291, ω -> 40.0271, T0 -> 125.429} *)

You do not get a terribly good fit with the initial parameters:

Plot[model[T, E∞, E0, ω, C1, T0, 
    C2, α, β][1] /. nlm["BestFitParameters"], {T, 130, 
  335}, Epilog -> {Red, PointSize[0.01], 
   Point /@ Take[data, Length[data]/2][[All, {1, 3}]]}]
Plot[model[T, E∞, E0, ω, C1, T0, 
    C2, α, β][2] /. nlm["BestFitParameters"], {T, 130, 
  335}, Epilog -> {Red, PointSize[0.01], 
   Point /@ Drop[data, Length[data]/2][[All, {1, 3}]]}]

Mathematica graphics Mathematica graphics

Looking at the correlation matrix, we see that T0, ω, C1 and C2 are very strongly correlated, suggesting that you need to have very good initial estimates for these parameters, or better yet, you need to simplify your model.

nlm["CorrelationMatrix"] // MatrixForm

Mathematica graphics

Community
  • 1
bobthechemist
  • 19,693
  • 4
  • 52
  • 138
3
data = {#, {#2, #4}} & @@@ Join[dataRe, dataIm, 2];

Ok, maybe I'm missing something but it seems there is no built in function to fit complex functions. So we have to create one:

model[T_, E∞_, E0_, ω_, C1_, T0_, C2_, α_, β_] := E∞ + (E0 - 
  E∞)/(1 + (I ω 10^(-((C1 (T - T0))/(C2 + (T - T0)))))^α)^β;

sol = FindMinimum[
       Norm[Flatten[
        ({Re[#], Im[#]} &[model[#, E∞, E0, ω, C1, T0, C2, α, β]] - #2) & @@@ data
       ]],
      {{α, 0.2}, {β, 0.6}, {E0, 4}, {E∞, 8000}, {C1, 17}, {C2, 50}, {ω, 10}, {T0, 110}}]

{122.628, {α -> 0.303236, β -> 9.03512, E0 -> 10.3146, E∞ -> 7999.98, C1 -> 21.383,
   C2 -> 36.8504, ω -> 9.93816, T0 -> 121.931}}

With[{opt = Sequence[PlotRange -> All, Axes -> False, Frame -> True, ImageSize -> 400, 
                     PlotStyle -> Thick, BaseStyle -> PointSize@.01]},
 Row[{
   Plot[Re@model[x, E∞, E0, ω, C1, T0, C2, α, β] /. sol[[2]], {x, 130, 335}, 
        Epilog -> {Point[dataRe]}, opt, PlotLabel -> "Re part"],
   Plot[Im@model[x, E∞, E0, ω, C1, T0, C2, α, β] /. sol[[2]], {x, 130, 335}, 
    Epilog -> {Point[dataIm]}, opt, PlotLabel -> "Im Part"]
   }]]

enter image description here

It is not perfect but this is the way. Try adjust initial values for example.

Kuba
  • 136,707
  • 13
  • 279
  • 740
  • I'm a freshman and I cannot read you code. I just copy the code and cannot get the result.Could you give me more details. – Yuuhsing Tuan Jan 28 '14 at 09:34
  • I got this:FindMinimum::nrnum: "函数值 [Sqrt](Abs[-887.339+Im[(7000. +Times[<<2>>])[135.,7000.,10.,10.,17.,120.,50.,0.3,9.]]]^2+Abs[-797.248+Im[(7000. +Times[<<2>>])[136.,7000.,10.,10.,17.,120.,50.,0.3,9.]]]^2+<<48>>+<<350>>) 不是位于 {[Alpha],[Beta],E0,E[Infinity],C1,C2,[Omega],T0} = {0.3,9.,10.,7000.,17.,50.,10.,120.} 的一个实数. " – Yuuhsing Tuan Jan 28 '14 at 10:09
  • @YuuhsingTuan Hello again, what the code does is calculating a vector: {Re@model(x_i), Im@model(x_i)}-data(x_i). Then we've got {{dRe1, dIm1}, {dRe2, dIm2}...}. Next Flatten and Norm produces: Sqrt[dRe1^2 + dIm1^2 + dRe^2 +...] and such expression is minimalzed with FindMinimum. It isn't the best, usually what is minimalized (LSQ) is D1^2 + D2^2..., you can modify. This shouldn't affect much. What can however, is changing initial values and/or model. It simply doesnt look like it can fit both now. You can also perform those procedures for model and data after taking double Log. – Kuba Jan 29 '14 at 06:00
  • your second picture should be “point［dataIm］”.And then the result is very good.Thanks a lot. – Yuuhsing Tuan Jan 29 '14 at 06:06
  • @YuuhsingTuan Ha, right :D so it does fit :) Thanks. Nonetheless my comments are still valid for the future ;) Good luck. – Kuba Jan 29 '14 at 06:11
  • Careful, Set your PlotRange to {0,60} and you'll note that this fit is about the same as mine. – bobthechemist Jan 29 '14 at 14:20
  • @bobthechemist Hi :) yes I agree, earlier there was the shift that looked terrible, that's why I'm happy now :P. imo to get a good fit one have to do this on double log data and model. To many parameters now and too high powers. – Kuba Jan 29 '14 at 14:23
  • I agree, and I figured you knew that. Just needed to go down on record for the OP since the different scale on my solution makes it "look bad". – bobthechemist Jan 29 '14 at 14:30