Finding all shortest paths between two vertices

Question

The built-in FindShortestPath and GraphDistance functions find the shortest path between two particular vertices in a graph. I can't think of a simple way to finding all shortest paths between two vertices. Any ideas?

My graph has weighted edges and the weights are arbitrarily large, so I'm dead against mapping weighted edges to many unweighted edges.

Motivation: I have a graph of city traffic routes from point A to point B. I'd like to take the union of shortest paths from A to B to get a subgraph that, I posit, contains (many of) the most frequented intersections.

This is a good question. The system must have at least some internal implementation for use in calculating the betweenness centrality, but I can't seem to find a user-accessible function. — Szabolcs, Apr 11 '12 at 07:22
A brute-force way to do it would be to break the path found by removing one of the edges of the shortest path, calculating the shortest path again, and if it has the same length, it's another shortest path of the original graph. You would have to do that for each edge of the shortest path, as well as recursively (i.e. for the newly found shortest path remove further edges; however here it should be sufficient to remove edges which are not also part of the original shortest path). — celtschk, Apr 11 '12 at 09:00
There is similar question http://stackoverflow.com/questions/2819347/dijkstras-algorithm-to-find-all-the-shortest-paths-possible . The third answer is not a bad idea. — PlatoManiac, Apr 11 '12 at 09:09
@celtschk, that depends on the problem, but something like this: Nearest[{1, 2, 4, 8, 16, 32}, 20, All]. You can specify a metric and/or create a NearestFunction. But all this needs more information in the question - an example would help. — , Apr 11 '12 at 09:09
@ruebenko: The problem is of course that of the question: Finding all shortest paths between two vertices of a given graph. Do you possibly think of enumerating all possible non-intersecting paths (an exponentially growing set!) and using Nearest to select those with length equal to GraphDistance? I don't think that would give a solution in acceptable time for moderately complex graphs. Anyway, the question already contains all information needed to define the problem. Indeed, even the first sentence of my comment already does, and so does the title of the question. — celtschk, Apr 11 '12 at 09:28
The documentation for BreadthFirstScan has an example of this problem under Examples-Applications-Shortest Path Applications. — Simon Woods, Apr 11 '12 at 09:31
Thinking about it, to get the union of shortest paths you probably don't need the set of shortest paths. I think the following algorithm should give you the union: Step 1: For each node, calculate the graph distance both to the start vertex A and the destination vertex B (let's call those values the A-distance and B-distance of that vertex). Step 2: Remove all edges whose weight is not both the difference between the A-distances of the vertices it connects and the difference between the B-distances. If I'm not wrong, the resulting graph should be exactly the union of all shortest paths. — celtschk, Apr 11 '12 at 09:43
@SimonWoods The example with BreadthFirstScan works for very small toy problems but even for GridGraph with dimension $12 \times 14$ memory consumption increases with out bound. — PlatoManiac, Apr 11 '12 at 09:57
@SimonWoods That's worth posting as an answer despite the high memory usage. It shouldn't be lost in the comment jungle. — Szabolcs, Apr 11 '12 at 13:56
@SimonWoods Thanks for the response! But irrespective of memory usage, that method would work only for unweighted graphs. — rjkaplan, Apr 11 '12 at 15:35
@rjkaplan I updated my shortest path solution with a directional graph. — DavidC, Apr 15 '12 at 18:58
@rjkaplan as you haven't accepted the answers would you please tell me how you solve the problem?Did you code it separately? — Alex, Oct 27 '13 at 19:13
My apologies! I have just accepted one of the solutions. I forgot to do so. — rjkaplan, Oct 27 '13 at 22:02

DavidC · Accepted Answer · 2015-08-30T12:48:55.190

Directed Shortest Paths

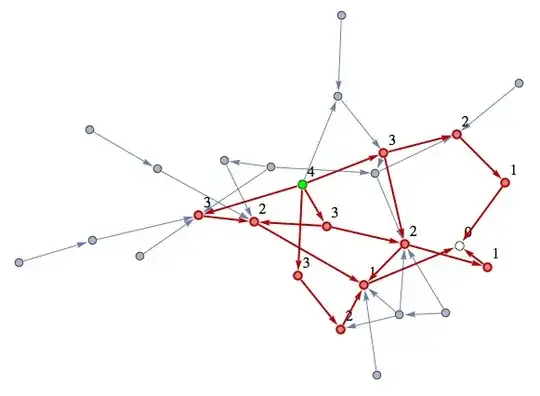
Here's a friendly amendment to Heike's solution that shows the distance remaining to the finish vertex (in white). The starting vertex is green. Edges are directed to show the appropriate direction toward the finish. According to the documentation on GraphDistance, "For a weighted graph, the distance is the minimum of the sum of weights along any path between s and t." So it should automatically work with weighted graphs.

First, here's Heike's routine, which does most of the heavy lifting, with a simple tweak to produce directed edges:

paths[gr_, {i_, j_}] := 
  Module[{sub, dist, indices, dd, nbrs}, dist = GraphDistance[gr, i, j];
  indices = {};
  dd = dist;
  Reap[Nest[Function[{vv}, dd -= 1;
  nbrs = VertexList[NeighborhoodGraph[gr, #]] & /@ vv;
  nbrs = Pick[#, GraphDistance[gr, #, j] & /@ #, dd] & /@ nbrs;
  Sow /@ Flatten[Thread /@ Thread[vv \[DirectedEdge] nbrs]];
  Union[Flatten[nbrs]]], {i}, dist]][[2, 1]]]

The following produces the directional routes. Numbers refer to GraphDistance from the current vertex to the finish vertex.

gr = RandomGraph[{30, 40}];
ends = {1, 30};
sub = paths[gr, ends];
e = EdgeList[gr] /. {x_ \[UndirectedEdge] y_ /; 
 GraphDistance[gr, x, 30] < GraphDistance[gr, y, 30] :> y \[DirectedEdge] x, 
   x_ \[UndirectedEdge] y_ /; 
 GraphDistance[gr, y, 30] <= GraphDistance[gr, x, 30] :>  x \[DirectedEdge] y}
gr1 = Graph[e, ImagePadding -> 15];

HighlightGraph[gr1, {Graph[sub], Style[1, Green], Style[30, White]}, 
 VertexLabels ->  Table[i -> Style[GraphDistance[gr1, i, 30], 16], {i, 
    Union[Level[sub, {-1}]]}], 
    VertexSize -> {1 -> Large, 30 -> Large}, 
    GraphHighlightStyle -> "Thick", ImagePadding -> 15]

directed graph

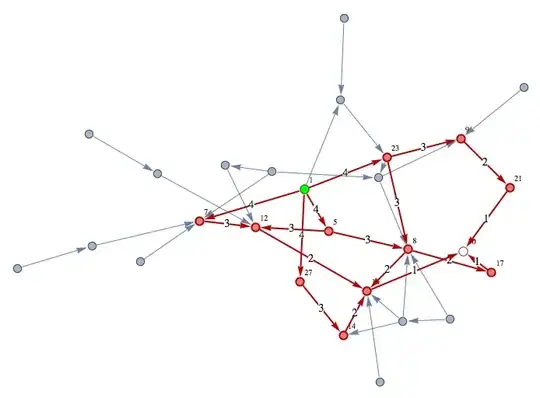
Below is a variant that displays (a) the vertex indices (small font size) and the distance from the finish vertex on the EdgeLabel (large font).

HighlightGraph[gr1, {Graph[sub], Style[1, Green], Style[30, White]}, 
   VertexLabels -> (v = Union[Level[sub, {-1}]]) /. {i_Integer :> (i -> i)},
   EdgeLabels -> sub /. {x_ \[DirectedEdge] y_ :> (x \[DirectedEdge] y) -> 
   Style[ GraphDistance[gr, x, 30], 14, Background -> White]},
   VertexSize -> {1 -> Large, 30 -> Large}, 
   GraphHighlightStyle -> "Thick", ImagePadding -> 15, ImageSize -> 600]

directed graph 2

Any such crossing can be handled by recognizing that there are two or more ways to reach it, all have the same length, and so the problem can be split into subproblems. Specifically, we'll have the Cartesion product of min paths from start to crossing and min paths from crossing to finish. Also one must account for min paths that do not hit the crossing vertex. All that said, labeling by distance to finish seems like a useful thing to have. — Daniel Lichtblau, Apr 12 '12 at 16:53
I'm wondering about "Any such crossing can be handled by recognizing that there are two or more ways to reach it, all have the same length". There may be only one way to reach the crossing (from a pre-selected start node); namely, if the in-degree is one. Note: I'm considering the union of shortest paths to be a directed sub-graph. By the way, is it possible for MMA to diagram a graph with a mix of directed and undirected edges. (I know multi graphs are not supported, but I would have thought that as long as there are no loops, and no more than a single edge between a pair of vertices...) — DavidC, Apr 12 '12 at 17:34
Correct about in-degree of one. I should have been more explicit. I had in mind the case where you cannot get to the finish minimally by taking ANY of the edges leading out (that is, not the one you took in to the vertex). This was in accord with your concern that one might have to choose from amongst a proper subset, which does not happen when in-degree is one. — Daniel Lichtblau, Apr 12 '12 at 18:23
This is nice, but it only works for graphs with unweighted edges, right? I wonder why this has been accepted seeing that the OP specifically asks for weighted edges. — Martin Ender, Aug 29 '15 at 22:04
It should work with weighted edges. From the documentation on GraphDistance: "For a weighted graph, the distance is the minimum of the sum of weights along any path between s and t." — DavidC, Aug 30 '15 at 12:47

score 16 · Answer 2 · answered Apr 11 '12 at 13:57

To get the union of the shortest paths from i to j in graph gr you could do something like this

paths[gr_, {i_, j_}] := Module[{sub, dist, indices, dd, nbrs},
  dist = GraphDistance[gr, i, j];
  indices = {};
  dd = dist;
  Reap[Nest[
     Function[{vv},
      dd -= 1;
      nbrs = VertexList[NeighborhoodGraph[gr, #]] & /@ vv;
      nbrs = Pick[#, GraphDistance[gr, #, j] & /@ #, dd] & /@ nbrs;
      Sow /@ Flatten[Thread /@ Thread[vv \[UndirectedEdge] nbrs]];
      Union[Flatten[nbrs]]
      ], {i}, dist]][[2, 1]]]

This method works by selecting all neighbours of i whose distance to j is one less than the minimal distance from i to j. For each vertex in this list we then select the neighbours whose distance to j is two less than the minimal distance, etc. until we reach j.

Usage

gr = RandomGraph[{30, 50}];
ends = {1, 30};
sub = paths[gr, ends];
HighlightGraph[gr, {Graph[sub], Style[ends, Green]}]

Mathematica graphics

Nice work, but there is a directionality issue to be considered. First, the start vertex and and end vertex need to be distinguished. In addition, I believe the highlighted edges need to be directed edges. Otherwise, the "driver" in the middle of traffic cannot necessarily know which direction to take when arriving at a vertex with degree >1. (Some edges may lead back toward the start; others may lead towards the finish.) — DavidC, Apr 12 '12 at 02:30

Dr. belisarius · Answer 3 · 2012-04-11T17:30:37.817

findMinPathsPoints[k_, ends_] := Module[{dist},
   dist = (GraphDistance[k, #[[1]]] + GraphDistance[k, #[[2]]]) &@ends;
   Complement[Flatten@Position[dist, Min[dist]], ends]];

(*Usage*)

n = 50;
points = {1, 10};
k = PetersenGraph[n, IntegerPart[n/4]]

Subgraph[k, Range@VertexCount@k, VertexStyle -> 
          Join[
              (# -> Red &)    /@ points, 
              (# -> Yellow &) /@ findMinPathsPoints[k, points]]]

enter image description here

score 9 · Answer 4 · answered Jan 19 '15 at 16:04

9

With V10, you can use a combination of FindPath and GraphDistance. A (hopefully) self-explanatory example:

g = RandomGraph[{15, 44}, VertexLabels -> "Name"];
s = 1;
t = 2;
FindPath[g, s, t, {GraphDistance[g, s, t]}, All]
HighlightGraph[g, %]

In short, we find all paths between $s$ and $t$ of distance $d(s,t)$.

answered Jan 19 '15 at 16:04

Juho

1,825
1
18
32

Yes this is very effective. – apg Nov 08 '19 at 08:53

Finding all shortest paths between two vertices

4 Answers4

Linked

Related