How can I plot a function that is the sum of another function?

Question

I plotted m[t], but actually what I want to plot is g[t], which is a summation of m[t] from 0 to 19 seconds. But when I plot g[t], I get dots. On the picture, what I want is on the right, I don't want the dots, so I guess list plot is not the way to go. How should I plot g to look like the picture I have to the right;

enter image description here

EDIT

My code;

period = 1;                                     
beta = 0.05;
An = List[{-1 , 1, -1, +1, -1, 1, -1, -1, 1, -1, 1, 1, 1, -1, 1, 1, -1, 1, -1, -1}];
sinch[t_] := (Sin[(Pit - tperiod)/period])/(Pi* t);

m[t_] := 
  An * sinch[t] * (Cos[(Pibetat - t*period) / period] / 
    (1 - (4beta^2  (t - t*period)^2 )/period^2 ));
Plot[{m[t]}, {t , 0, 19}]
g = Sum[m[t], {t, 1, 20}];
ListPlot[g]

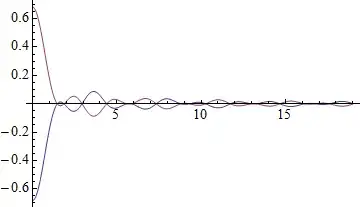
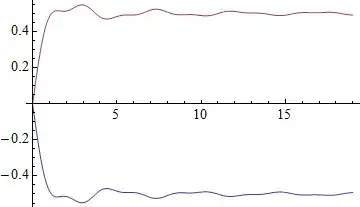
Can you post your code here, not a snapshot? P.S. maybe Sum instead of sum? — ybeltukov, Jan 29 '14 at 20:03
If you define m[t] as m[t_] := sinch[t]*(Cos[(Pi*beta*t - t*period)/ period]/(1 - (4*beta^2*(t - t*period)^2)/period^2));, then the plot Plot[m[t], {t, 0, 19}] looks very much like what you show on the right of the image shown in your question — m_goldberg, Jan 30 '14 at 03:08
I voted to leave closed because Total[m[t], 2] is almost zero everywhere. Try Plot[Total[m[t], 2], {t, 0, 19}] to see it — Dr. belisarius, Jan 30 '14 at 04:03
Yves Klett, your way gives me what I want for m(t), but then you did not multiply with the "An" , because An comes out of the summation and multiplies at the end. — user124627, Jan 30 '14 at 16:49

score 3 · Answer 1 · edited Apr 13 '17 at 12:55

Your usage of Sum gives you only a single sum, not a cumulative one. I shall assume that you want to integrate your function.
Your function produces many identical lines; I shall keep only two unique ones.
You have an extraneous List level in An; I shall remove it.
You probably want the option PlotRange -> All in the Plot, so that you see everything.
I shall add Evaluated -> True to give independently styled lines. See: Plot draws list of curves in same color when not using Evaluate. I use Evaluated -> True rather than Evaluate to properly localize the plot variable.⁽¹⁾ ⁽²⁾

Code:

period = 1;
beta = 0.05;
An = {-1, 1};

sinch[t_] := (Sin[(Pi*t - t*period)/period])/(Pi*t);

m[t_] := An*sinch[t]*(Cos[(Pi*beta*t - t*period)/
       period]/(1 - (4*beta^2*(t - t*period)^2)/period^2));

Block[{t},
  g[t_] = Integrate[m[t], t] // Chop;
]

Plot[m[t], {t, 0, 19}, PlotRange -> All, Evaluated -> True]

Plot[g[t], {t, 0, 19}, PlotRange -> All, Evaluated -> True]

Result:

enter image description here

How can I plot a function that is the sum of another function?

EDIT

1 Answers1