How to select all elements above the main diagonal of matrix? I need to create a list of them.
7 Answers
The Diagonal command has a second argument that allows listing the elements of the jth superdiagonal. So we can map over all the superdiagonals:
n = 4;
mat = Array[a, {n, n}];
Flatten[Diagonal[mat, #] & /@ Range[n-1]]
which gives a list of all the elements above the diagonal:
{a[1, 2], a[2, 3], a[3, 4], a[1, 3], a[2, 4], a[1, 4]}
-
1Niiiiice, I learned something new – Rojo Jan 30 '14 at 01:49
Let's use Span with Part:
mat=RandomInteger[{0, 100}, {5, 5}];
Flatten[mat[[#, # + 1 ;;]] & /@ Range[5]]
- 10,922
- 1
- 32
- 69
I believe that kale's approach is the best, but it can be improved with Join which is considerably faster than Flatten on packed lists, and it is a bit cleaner when written with Array:
Join @@ Array[mat[[#, # + 1 ;;]] &, n - 1]
To make this into a fast function it seems that one needs a Hold attribute (pass-by-reference):
SetAttributes[aboveDiag, HoldFirst];
aboveDiag[a_] := Join @@ Array[a[[#, # + 1 ;;]] &, Length[a] - 1]
Compare timings (done in v7) with bill s's code and R.M's upperElements function. (I left MatrixQ out of upperElements in these tests to eliminate overhead and level the field.)
n = 5000;
mat = RandomInteger[999, {n, n}];
Flatten[Diagonal[mat, #] & /@ Range[n - 1]] // Timing // First
upperElements[mat] // Timing // First
aboveDiag[mat] // Timing // First
0.32760.1872
0.02308
Not quite as superior on non-packed data, but still a good bit faster than the others.
n = 2000;
mat = Developer`FromPackedArray @ RandomInteger[999, {n, n}];
Flatten[Diagonal[mat, #] & /@ Range[n - 1]] // Timing // First
upperElements[mat] // Timing // First
aboveDiag[mat] // Timing // First
0.14040.0998
0.02308
Inspired by rasher's use of MapIndexed, here is another one that tests the fastest on unpacked data on my system (using last mat above):
Join @@ MapIndexed[Drop[#, #2[[1]]] &, mat] // Timing // First
0.01996
It is much slower than aboveDiag on packed data.
- 271,378
- 34
- 587
- 1,371
-
1
Joinis not only faster but better than flatten (with no second arg) if the matrix can have list elements – Rojo Jan 30 '14 at 06:47 -
-
2Nice tuning, as usual! For non-huge arrays, I use (filter matching this particular problem in this case):
FilterRules[ArrayRules[yourArrayHere], {a_, b_} /; b > a]Just seems... neat, if not a hot-rod. – ciao Jan 30 '14 at 07:53 -
1
-
I don't know but I've ran this and
upperElemetsandaboveDiaghave comparable timings forPackedArray. Also in packed case myPickis two times faster, unless I'm doing something wrong. – Kuba Jan 30 '14 at 08:35 -
@Kuba: Not even in the same zip-code as
aboveDiagin my tests. Even an unlikely-lookingMapIndexedimplementation smokes thePickmethod (I tried that exactPickway early on). – ciao Jan 30 '14 at 09:06 -
@Kuba Very interesting. I know that
Pickwas improved after version 7, but I didn't expect it to be twice as fast as these alternatives. Also, ifPartandSparseArraynow perform equally I wonder ifParthas gotten slower, orSparseArrayhas gotten faster; hopefully the latter. – Mr.Wizard Jan 30 '14 at 09:06 -
@rasher Which version are you running, and are you using a packed arrays? – Mr.Wizard Jan 30 '14 at 09:07
-
@Mr.Wizard: 9.0.1,W32, on the goofing-off cigarnetbook as usual. Yes, testing with packed arrays as generated by
RandomInteger. – ciao Jan 30 '14 at 09:10 -
WinXP V9.0.1.0, Packed test:
0.593750, 0.421875, 0.312500andPick: 0.171875– Kuba Jan 30 '14 at 09:10 -
@Mr.Wizard: I'm curious what the following does in your environment. It seems to trade blows with
aboveDiagin my limited testing with packed, and dusts it pretty well with unpacked/symbolic/string arrays:Join @@ MapIndexed[yourArrayHere[[#2[[1]], #1]] &, Span @@@ Transpose[{Range[2, n], ConstantArray[n, n - 1]}]](n s/b length of array of course) – ciao Jan 30 '14 at 12:17 -
@rasher I get exactly the same timings from both
aboveDiagand your code, on both packed integers and strings. I wonder whyMapIndexedis faster on your system. How does this compare?:Join @@ MapIndexed[mat[[#2[[1]], #1 ;;]] &, Range[2, n]]and also:Join @@ MapIndexed[Drop[#, #2[[1]]] &, mat]. (The latter is the fastest on string data on my system; I shall add it to my answer.) – Mr.Wizard Jan 30 '14 at 12:42 -
@Mr.Wizard: On packed, both get same timing +/- noise as my goofy one (span-building was left from other experiments). All three (those & mine) avg. 2-3X faster on unpacked (using
Developer``FromPackedArrayto unpack same test arrays) vsaboveDiag, all three and the latter smokePickin all cases I tested. Interesting, probably CPU APU & under-the-cover auto-paralleling differences... – ciao Jan 30 '14 at 21:51
Update:
Statistics`Library`UpperTriangularMatrixToVector is faster than all posted methods on packed data. Using the set up from @Mr.Wizard's answer:
n = 4000;
mat = RandomInteger[999, {n, n}];
(res0 = Statistics`Library`UpperTriangularMatrixToVector@mat) // Timing // First
0.027995
(res1 = Join @@ MapIndexed[Drop[#, #2[[1]]] &, mat] )// Timing // First
0.158976
(res2 = aboveDiag[mat] )// Timing // First
0.250961
res0 == res1 == res2
True
On unpacked data, it is slower than Join@@MapIndexed[...] but faster than aboveDiag:
n = 2000;
mat = Developer`FromPackedArray @ RandomInteger[999, {n, n}];
(res0 = Statistics`Library`UpperTriangularMatrixToVector@mat) // Timing // First
0.096986
(res1 = Join @@ MapIndexed[Drop[#, #2[[1]]] &, mat] ) // Timing // First
0.029996
(res2 = aboveDiag[mat] ) // Timing // First
0.384942
res0 == res1 == res2
True
Previous version:
n = 4; mat = Array[a, {n, n}];
Statistics`Library`UpperTriangularMatrixToVector @ mat
{a[1, 2], a[1, 3], a[1, 4], a[2, 3], a[2, 4], a[3, 4]}
Also
mat[[##]] & @@@ Subsets[Range[n], {2}]
Extract[mat, Subsets[Range[n], {2}]]
{a[1, 2], a[1, 3], a[1, 4], a[2, 3], a[2, 4], a[3, 4]}
- 394,356
- 18
- 477
- 896
n = 4;
mat = Array[a, {n, n}];
Flatten@Table[If[j > i, mat[[i, j]], {}], {i, n}, {j, n}]
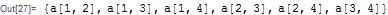
- 143,286
- 11
- 154
- 359
Here's an option for square matrices using undocumented properties of SparseArray, which clocks in slightly faster for me than Mr.Wizard's solution:
upperElements[mat_?MatrixQ] := With[{n = Length@mat},
SparseArray[UpperTriangularize[mat, 1]]["NonzeroValues"] ~PadRight~ (n (n - 1)/2)];
This constructs a sparse strictly upper triangular matrix, extracts the non-zero values and then pads it to a length of $n(n-1)/2$, where $n$ is the dimension of the matrix (to account for any upper element that might have been zero).
For non-square matrices of dimension $m\times n$, you might try using a closed form expression for the number of upper triangular entries (see here, for instance).
-
How come I didn't think of padright and worried about deleting extra zeros. +1 – Rojo Jan 30 '14 at 07:01
-
On my system (v7) this is about six to seven times slower than
aboveDiagwithn = 5000; mat = RandomInteger[999, {n, n}];(and leaving outMatrixQfor a fair test). What data are you testing with, and what timings do you get for my data in v9? – Mr.Wizard Jan 30 '14 at 07:04 -
@Mr.Wizard I don't have the timings right now, but it was very close to yours, but a wee bit faster. I see from the comments under yours that Kuba got similar results. I don't have v7 installed, so I can't confirm your findings. – rm -rf Jan 30 '14 at 16:55
Variation of Nasser answer:
n = 4;
m = Array[a, {n, n}];
Join @@ Table[m[[ i, j]], {i, n}, {j, i + 1, n}]
{a[1, 2], a[1, 3], a[1, 4], a[2, 3], a[2, 4], a[3, 4]}
just another way:
Join @@ Pick[
m,
UpperTriangularize[ConstantArray[1, {n, n}], 1],
1]
- 136,707
- 13
- 279
- 740