Find nearest distance of an interior point from perimeter

Question

By definition, the interior point is a point inside an arbitrary region like this:

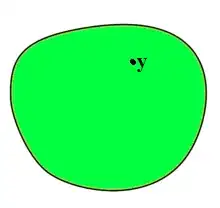
enter image description here

In picture above, $y$ is an interior point of region. My question is how to find the distance of an interior point from it's boundary?

I have this Idea: By using the polygons, we can approximate the perimeter of region by a n-gon (n is large enough). Then by saving the coordinates of perimeter in two vectors, say $x$ and $y$, and use Nearest command we can find nearest point of perimeter from interior point ($y$).

I created data matrices (find from here) in MATLAB and import to Mathematica.

imp = Import["PI.mat", "LabeledData"];
X = "KP" /. imp;
Y = "KI" /. imp;

But I can't know how to use Nearest command when we have large vectors like X and Y :

Nearest[{Flatten@X, Flatten@Y}, {3, 1.5}]

An error appears, because Flatten@X, Flatten@Y and {3, 1.5} are not the same length.

Not bad idea, not sure exactly what is in X Y but maybe you want: Nearest[Transpose@{X, Y}, {1.5, 3}]? — Kuba, Feb 03 '14 at 08:22
@Kuba XandYare two simple vectors. I used that, but not sure it's correct. But what does it (Transpose`) do? — user2667048, Feb 03 '14 at 08:32
Did you look at RegionDistance and SignedRegionDistance? — Sjoerd Smit, Aug 11 '23 at 14:29

score 8 · Answer 1 · answered Feb 03 '14 at 09:02

You can compute the distance to all points within the shape in a single pass using DistanceTransform. I was unable to load your data file in Mathematica 7 so I will use an arbitrary shape as an example:

bsf = BSplineFunction[{{0, 0}, {1, 0}, {2, .5}, {1, 1}, {0, 1}}, SplineClosed -> True];

pts = Table[bsf[x], {x, 0, 1, 0.01}];

gr =
 Graphics[{White, Polygon[pts]},
  Background -> Black,
  ImageMargins -> 0,
  PlotRangePadding -> 0,
  ImageSize -> 500
 ]

dist = ImageData @ DistanceTransform[gr];

dist // MatrixPlot

enter image description here

Obviously extracting the correct value(s) will take some scaling, but I don't have time at the moment to work it out. Look at Rescale however.

ciao · Accepted Answer · 2014-02-03T09:08:24.197

4

Assuming I interpreted your data correctly...

imp = Import["C:\\Users\\Rasher\\Downloads\\" <> "PI.mat", "LabeledData"];

(* get data into flat lists *)
X = "KP" /. imp // Flatten;
Y = "KI" /. imp // Flatten;

(* turn into X,Y point-sets *)
pts = Transpose[{X, Y}];

(* Find some point to boundary of poly *)
Nearest[pts, {3, 1.5}]

(*  {{2.67062, 2.7767}}   *)

edited Feb 03 '14 at 09:08

answered Feb 03 '14 at 08:36

ciao

25,774
2
58
139

Sorry I made a mistake. Please correct {1.5,3} to {3,1.5}. ({1.5,3} is not interior point) Thanks for detailed answer. – user2667048 Feb 03 '14 at 08:40
I think it is not sufficient to compute the distance to the nearest point since the nearest line may be considerably closer. – Mr.Wizard Feb 03 '14 at 09:08
@user2667048:done – ciao Feb 03 '14 at 09:09
@Mr.Wizard Can you give an example? – user2667048 Feb 03 '14 at 09:11
@user2667048 I mean something like this: Graphics[{Polygon[{{1, 0}, {0, Sqrt[3]}, {-1, 0}}], Red, PointSize[Large], Point[{-0.4, 0.7}]}] -- I assume you want the distance to the edge, not one of the vertexes, correct? – Mr.Wizard Feb 03 '14 at 09:16
@Mr.Wizard Yes. you're right. But how I can't understand why "it's not sufficient to compute the distance to the nearest point"? In your example the nearest point obtain by drawing perpendicular line from red point to left side. – user2667048 Feb 03 '14 at 09:28
@user2667048 I'm a bit distracted at the moment and I may be reading rasher's answer wrong, but I think he is only returning the nearest vertex in the data. I don't see a computation of distance at all, and especially not distance to the nearest point along the closest line. (I hope that makes sense.) Anyway, IMHO neither existing answer is complete at this time. – Mr.Wizard Feb 03 '14 at 09:32
1

@Mr.Wizard: No, you're interpreting it right, I read the question as the OP wants the nearest point contained in the point-set. If in fact the OP means the nearest point of the connected polygon described by the point-set, my answer is not want they want (hence my caveat re: interpretation), and I'll delete it. – ciao Feb 03 '14 at 09:38
@rasher Thanks for clarifying. – Mr.Wizard Feb 03 '14 at 10:19
@user2667048: If I misinterpreted your intent, please comment, I can walk you through simple addition to do distance to polygon line... – ciao Feb 04 '14 at 09:03
1

@rasher Actually no, you interpreted well. But how can we find nearest point from polygon line in a simple way? – user2667048 Feb 04 '14 at 12:48
Do you know how to use Norm? If so, use the example to find the nearest point (a vertex of your polygon) then use Norm and the simple associated calculations to find the closest point on the two line segments from that vertex. If you're not familiar with the process, reply and I'll whip up the code and update my answer. – ciao Feb 05 '14 at 09:08

score 3 · Answer 3 · answered Mar 20 '17 at 14:40

RegionNearest can also be an option

imp = Import["C:\\Users\\Ali Hashmi\\Downloads\\PI.mat","LabeledData"];
X = "KP" /. imp;
Y = "KI" /. imp;
threadeddata = Transpose[{Flatten@X, Flatten@Y}];
RegionNearest[Line@threadeddata, {3, 1.5}]

(* {2.67041, 2.77665} *)

score 0 · Answer 4 · answered Aug 11 '23 at 14:02

Since the original data is not accessible anymore, a boundary is setup using CirclePoints with randomness added. After that BSplineFunction is used to create a smooth contour. Discretizing the graphic sets up the region.

SeedRandom[1234];
n = 6; (* Can experiment with more points *)
(pts = CirclePoints[{2, 0}, n]
   + RandomReal[1, {n, 2}]);(*//ListPlot[#,AspectRatio->Automatic]&*)
bsf = BSplineFunction[pts, SplineClosed -> True];
g1 = ListLinePlot[Table[bsf[x]
    , {x, 0, 1, 0.01}]
   , AspectRatio -> Automatic];
mreg = DiscretizeGraphics[g1];
Manipulate[
 Show@{
   Region[Style[mreg, Black], Frame -> True]
   , Graphics[{
     {Red, AbsolutePointSize[6], 
      Point@{x + r Cos[θ], y + r Sin[θ]}
      , {Blue, AbsolutePointSize[6]
       , Point@
        RegionNearest[mreg, {x + r Cos[θ], y + r Sin[θ]}]
       , {Black, Dashed, Circle[{x, y}, r]}
       }
      }
     }
    , Frame -> True]
   }
 , {{x, 0.7}, -1 + r, 2.5 - r}
 , {{y, 0.5}, -1 + r, 2.5 - r}
 , {{r, 0.5}, 0.01, 1.2}
 , {{θ, 0}, 0, 2 π}
 , TrackedSymbols :> All
 ]

Find nearest distance of an interior point from perimeter

4 Answers4

Linked