3

  1. Use Euler's Method or the Modified Euler's to solve the differential equation ${dy/dt=y^2+t^2-1, y(-2)=-2}$ on $[- 2, 2]$. Take h = 0.2 (n = 20 iterations).

  2. See if Mathematica will give an analytic solution to this problem.

    If it does compare the analytic solution found in Problems 1 and 2.

    If Mathematica will not give an analytic solution, compare your solutions to the numerical solution on $[-2, 2]$ given by Mathematica.

For the first problem, I am confused of the interval is not $[0,2]$ but $[-2,2]$ I have no idea with these two problems, can anyone help me?

J. M.'s missing motivation
  • 124,525
  • 11
  • 401
  • 574
vicky1229
  • 31
  • 3

1 Answers1

6

Edit

I edited to replace h with N@h as suggested by MichaelE2, to prevent Mathematica slowdown if exact h is provided by the user.

Note for future users: I initially had a procedural approach posted, if you're interested in that method see the edit history. I present a Functional approach, this is Mathematica after all.

SetAttributes[eulerMethod, HoldAll];

eulerMethod[func_, {x_, x0_, xmax_}, {y_, y0_}, h_] := 
 Module[{EulerStep, hh = N@h},  
  EulerStep[{xi_, yi_}] := Module[{xold = xi, yold = yi, xnew, ynew}, 
    xnew = xold + hh; 
    ynew = yold + hh ReleaseHold[Hold[func] /. {HoldPattern[x] -> xold, 
          HoldPattern[y] -> yold}]; {xnew, ynew}];
      NestList[EulerStep, {x0, y0}, Round[(xmax - x0)/hh]
     ]
  ]

Usage

sol = eulerMethod[y^2 + t^2 - 1, {t, -2, 2}, {y, -2}, 0.2];

You can compare it to the built in NDSolve by plotting both in the range [-2, 2]

ListLinePlot[sol, Filling -> Axis]

Mathematica graphics

For NDSolve:

nd = NDSolve[{y'[t] == y[t]^2 + t^2 - 1, y[-2] == -2}, y[t], {t, -2, 2}];

Then

Plot[y[t] /. nd, {t, -2, 2}, Filling -> Axis]

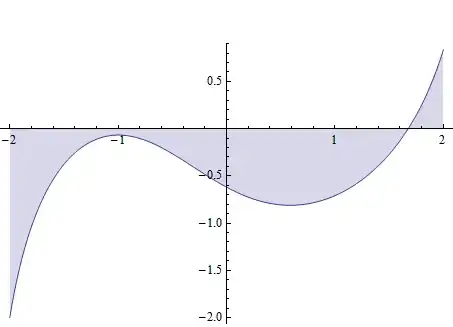
Mathematica graphics

Clearly, our eulerMethod needs more iteration (smaller step size) to get close to the more accurate NDSolve

If we increase the number of iterations (decrease h) we nail the accuracy

sol2 = eulerMethod[y^2 + t^2 - 1, {t, -2, 2}, {y, -2}, 0.01]

ListLinePlot[sol2, PlotStyle -> {Red, Thick}, Filling -> Axis, FillingStyle -> Darker@Green]

Mathematica graphics

Clearly, this looks very much like the result from NDSolve

You can get an exact solution using DSolve as follows:

DSolve[{y'[t] == y[t]^2 + t^2 - 1, y[-2] == -2}, y[t], t]
RunnyKine
  • 33,088
  • 3
  • 109
  • 176
  • @vicky1229, RunnyKine, You might want to consider apply N somewhere in case someone does eulerMethod[y^2 + t^2 - 1, {t, -2, 2}, {y, -2}, 1/100]. See also http://mathematica.stackexchange.com/questions/22042/nestlist-and-eulers-method/22048#22048. (+1) – Michael E2 May 18 '15 at 19:45
  • @MichaelE2, I just saw your comment I haven't been active in a while. I'll fix it. Thanks for pointing that out and for the upvote. – RunnyKine May 27 '15 at 05:31