Plotting a line segment from the degenerate case of an ellipse

Question

An ellipse degenerates into a line segment when the defining constant distance from the two foci is the actual distance between the two foci. The ellipse closes into a line segment.

The following code shows a family of concentric ellipses that should converge to a line segment when the constant is set to 5. However it doesn't plot the line segment even if I increase the MaxRecursion very high.

ContourPlot[Evaluate[Table[Sqrt[(x + 3)^2 + y^2] + Sqrt[x^2 + (y - 4)^2] == n, {n, 5, 
6, .01}]], {x, -4, 1}, {y, -1, 5}]

Is there someway to get Mathematica to actually plot the line segment of the degenerate case of an ellipse?

@Kuba That does work to draw a line segment. Thanks! So I guess Mathematica just can't recognize the degenerate case of the ellipse and I'll have to use that method in place instead? — David Caliri, Feb 06 '14 at 18:12

bill s · Answer 1 · 2014-02-06T18:41:22.590

You can get an ellipse almost at the center, but you will need to increase the number of points in the plot:

ContourPlot[Evaluate[Table[
   Sqrt[(x + 3)^2 + y^2] + Sqrt[x^2 + (y - 4)^2] == n, 
   {n, 5.0001, 6, .1}]], {x, -4, 1}, {y, -1, 5}, PlotPoints -> 200]

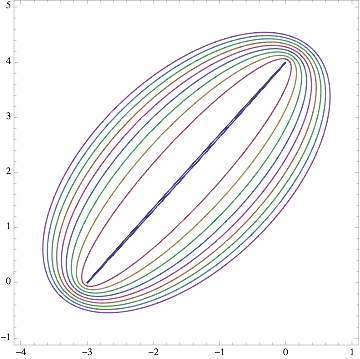
enter image description here

It looks even more line-like if you decrease n to 5.00002 and increase PlotPoints to 600, though this dramatically increases the time required to draw the plot.

Plotting a line segment from the degenerate case of an ellipse

1 Answers1