Unset while running recursion

Question

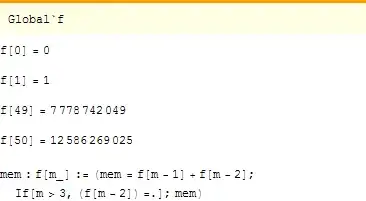
I am trying to run a recursive definition while at the same time clearing previously found values, so my memory is not completely consumed. I found this: How to clear parts of a memoized function? But it does not seem to be what I am looking for. I want to clear memorized values, while the recursion is running. I thought I could do something like this:

Block[{$IterationLimit = $RecursionLimit = ∞},f [m_]:= f [m] = f [m-1]+f [m-2]

f[0]=0

f[1]=1

If [m - 3 > 0, Unset[f[m-3]]]

But it does not work. I realize I could just use Fibonacci[n], but I am doing this to try to learn Mathematica not to study the Fibonacci sequence. Thank you for any help!

Sidenote, you aren't localizing RecursionLimit there. Plus, the variables are $RecursionLimit and $IterationLimit with a $ — Rojo, Feb 08 '14 at 18:13
A long time ago I played with using memoization while limiting memory use. It's described here. Search for memoization on that page. — Szabolcs, Feb 08 '14 at 21:29

score 9 · Answer 1 · answered Feb 08 '14 at 17:10

9

If I've understood the question correctly, you need to put the Unset inside the function definition, e.g.

mem : f[m_] := (
  mem = f[m - 1] + f[m - 2];
  If[m > 3, Unset@f[m - 2]];
  mem)

f[0] = 0;
f[1] = 1;

Now you can compute, say, f[50] and get the speed advantage of memoization, but only ever keeping the two values required for the next iteration.

f[50]
(* 12586269025 *)

?f

enter image description here

answered Feb 08 '14 at 17:10

Simon Woods

84,945
8
175
324

Awesome! Thank you, this is exactly what I was looking for! – user3116891 Feb 16 '14 at 03:12

score 6 · Answer 2 · edited Apr 13 '17 at 12:55

I realize that the Fibonacci sequence is merely an example, but since it is an example it might as well serve to show other approaches. Please see: Fibonacci Sequence Generator. In addition to those methods here is a Nest variation:

nx[{a_, b_}] := {b, a + b}

g[n_] := First @ Nest[nx, {0, 1}, n]

Array[g, 9, 0]

{0, 1, 1, 2, 3, 5, 8, 13, 21}

Only the last two values are kept for the next calculation, just like Simon's code. This is also quite a general method as you could perform any operation on the last n values. (Of course a method keeping all values, such as NestList or FoldList, would be better if you are building the fully array.)

Very good to know, thank you! – user3116891 Feb 16 '14 at 03:14 — user3116891, Feb 16 '14 at 03:14

Unset while running recursion

2 Answers2

Linked