15

Edit: since the upgrade to Mathematica 10, this problem seems solved

I just want to solve a system of partial differential equations, for example:

$$ \left\{ \begin{array}{l} \frac{\partial}{\partial a}[f(a, b, c)] = 4 \sin^2(b) \cos(c) \\ \frac{1}{a} \times \frac{\partial}{\partial b}[f(a, b, c)] = 4 \cos(c) \sin(2b) \\ \frac{1}{a \sin(b)} \times \frac{\partial}{\partial c}[f(a, b, c)] = -4 \sin(b) \sin(c) \\ \end{array} \right. $$

And when I try to solve this system in Mathematica, the output does not help:

    DSolve[
    {
        D[f[a, b, c], a] == 4 Sin[b]^2 Cos[c],
        (1/a) *D[f[a, b, c], b] == 4 Cos[c] Sin[2 b],
        (1/(a Sin[b]))*D[f[a, b, c], c] == -4 Sin[b] Sin[c]
    }, f[a, b, c], {a, b, c}]


(* DSolve[
    {
        Derivative[1, 0, 0][f][a, b, c] == 4*Cos[c]*Sin[b]^2,
        Derivative[0, 1, 0][f][a, b, c]/a == 4*Cos[c]*Sin[2*b],
        (Csc[b]*Derivative[0, 0, 1][f][a, b, c])/a == -4*Sin[b]*Sin[c]
    }, f[a, b, c], {a, b, c}] *)

Obviously, this output is useless… Probably I doing something wrong…

Thank you for your help

Note : The solution is $f(a, b, c) = 4a \sin^2(b) \cos(c) + K$ (K : the integration constant).

xzczd
  • 65,995
  • 9
  • 163
  • 468
mlpo
  • 879
  • 2
  • 7
  • 11
  • When DSolve returns unevaluated, it means that it couldn't solve the problem. From the documentation: "DSolve can find general solutions for linear and weakly nonlinear partial differential equations. Truly nonlinear partial differential equations usually admit no general solutions." While yours looks solvable, it probably just decides it can't do it. – Szabolcs Feb 14 '14 at 21:46
  • That's strange. Because this system has at least one solution : f(a, b, c) = 4a Sin[b]^2 * Cos[c] + K (K : the integration constant). – mlpo Feb 14 '14 at 21:49
  • Yes, I just solved it by hand. I still believe that Mathematica just can't do it. It probably doesn't have good support for PDEs. There's nothing wrong with your syntax. If you have doubts, you might contact support at wolfram.com and ask if there's a bug. – Szabolcs Feb 14 '14 at 21:54
  • Is it possible to solve this kind of system other than manually :D ? Maybe an other way… – mlpo Feb 14 '14 at 21:59
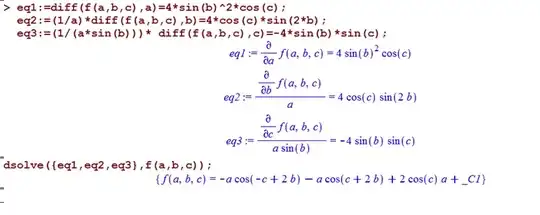
  • Can you explain why you want to do that, so we can give better advice? If the reason is that you have large expressions which are easy but very tedious to work with, then yes: you can use Mathematica's functions such as Integrate, TrigReduce, Simplify, etc. to get the mechanical parts done automatically, while you guide it through the complete procedure by hand. The Algebraic Manipulation Palette is useful for this type of work. – Szabolcs Feb 14 '14 at 22:04
  • In fact, the problem is not that I have large expressions but I have a lot of such systems to solve (they all have roughly the same size). However, they are quite different and numerous (more than 100). – mlpo Feb 14 '14 at 22:18
  • OK. So we established that this system that you showed is actually quite trivial to solve (by hand). If your other systems are also relatively simple, and all of the same form, maybe we could try to write a specialized solver which works for most of them. You could update the post with a few examples of such systems, as well as the most general form that fits all of them, and see if people have an idea for implementing a speclized solver for these. – Szabolcs Feb 14 '14 at 22:23
  • The problem is they are precisely very different from each other (some are trigonometric combinations, but others are larger and involve more complex expressions). They are not very long (always less than 10 equations) but not always trivial. – mlpo Feb 14 '14 at 22:29
  • 2
    Here is something more strange. Try DSolve[{D[f[a, b], a] == 0,(1/a) D[f[a, b], b] == 0},f[a, b], {a, b}] and it can't do it. Now remove the (1/a) from the second equation, (which is the same as multiplying both sides by a, then it solves it ! – Nasser Feb 14 '14 at 22:34
  • 1
    @Nasser Looks like you touched on the solution. If we bring the OP's PDE system into a form where the LHS only has the derivatives, Mma can solve the system: DSolve[{D[f[a, b, c], a] == 4 Sin[b]^2 Cos[c], D[f[a, b, c], b] == 4 a Cos[c] Sin[2 b], D[f[a, b, c], c] == -4 a Sin[b] Sin[b] Sin[c]}, f[a, b, c], {a, b, c}] You should post this as an answer, it's worth highlighting. – Szabolcs Feb 14 '14 at 22:37
  • 1
    @Szabolcs Yes, I was just trying to verify things...was planing to write something but have to make coffee first :) btw, Maple is able to solve it in its current form without rearranging: screen shot Mathematica graphics – Nasser Feb 14 '14 at 22:39
  • @Nasser I know you've looked at several algebra systems. Are you aware of any, besides Maple and Mathematica, that have some support for symbolic PDE (not ODE) solving? I'm just curious. – Szabolcs Feb 14 '14 at 22:51
  • @Szabolcs I am not really sure. I think Sage and Axiom and Fricas can. But maybe not Maxima, but I really can't be 100% sure without researching this. I only play with M and sometimes Maple. But good question. I googled little and do not see something on this now. Would require more time to find out. – Nasser Feb 14 '14 at 23:36

2 Answers2

16

One can get a hint of the issue by seeing that 

 DSolve[{1/a D[f[a, b], a] == 1, D[f[a, b], b] == 1}, f[a, b], {a, b}]

can't be solved, but 

 DSolve[{ D[f[a, b], a] == a, D[f[a, b], b] == 1}, f[a, b], {a, b}]
 (* {f[a, b] -> a^2/2 + b + C[1]}} *)

can. But there are the same system! (multiplying by a both sides of the first equation in the first case gives the second system). The first system, as written, is consistent. There is a test one can use to check the system of PDE's is consistent. Using Maple:

with(PDEtools):

eq1 := 1/a*diff(f(a,b),a) = 1:
eq2 := diff(f(a,b),b)     = 1:

ConsistencyTest({eq1,eq2});
(* true *)
dsolve({eq1,eq2},f(a,b));
(* f(a, b) = (1/2)*a^2+b+_C1 *)

May be DSolve got worried about singularity when a=0? I do not know. But noticing the above gives a hint on the solution. Simply rearrange terms so that the leading derivative term has unity as factor.

DSolve[{
  D[f[a, b, c], a] == 4 Sin[b]^2 Cos[c],
  D[f[a, b, c], b] == a 4 Cos[c] Sin[2 b],
  D[f[a, b, c], c] == -a Sin[b] 4 Sin[b] Sin[c]},
 f[a, b, c], {a, b, c}
 ]

(* {{f[a, b, c] -> C[1] + 4 a Cos[c] Sin[b]^2}} *)

By the way, there really should not be a need to do this rearrangement. Maple 17 can solve this as is

Mathematica graphics

The real question is: Why is the rearrangement needed? that is what the inquiring minds want to know :)

Nasser
  • 143,286
  • 11
  • 154
  • 359
  • isn't the answer do to with the fact that in the first form if a=0 or sin(b)=0 the equation is singular whereas it is not in the other form? For instance what happens if the boundary condition involve a=0 ? – chris Apr 09 '14 at 07:11
0

In Mathematica 10, one can use the original DSolve entry by embedding it within an Assuming

Assuming[a != 0, DSolve[. . .] ]
Mr.Wizard
  • 271,378
  • 34
  • 587
  • 1,371
shokutaku
  • 11
  • 1
    As mentioned in the question, the problem has been fixed since the update to Mathematica 10. You can get the right result with the original DSolve without any changes. – mlpo Feb 15 '17 at 01:34