Subtracting from a specific column

Question

I have a huge list with huge sublists of the form

list={{a,b,c,d},{e,f,g,h},{i,j,k,l}}

I am looking for a way to manipulate these sublists based on the positions of the elements. Something like

list/.{j_,k_,l_,m_}->{j-1,k,l,m}

but without having to write the whole pattern. Is there any way to specify such manipulation based on the position of the element? Something like

list/.#[[1]] & -> #[[1]] - 1 &

that would work?

Do you want (for example) to subtract one from the first element in each sublist? — Dr. belisarius, Feb 17 '14 at 18:56
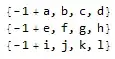
f[l_List] := {First@l - 1, Sequence @@ Rest@l}; f /@ list ? — Dr. belisarius, Feb 17 '14 at 18:59
@belisarius Yes, for instance. @Szabolcs Yes, Length@myoriginallist outputs 81 for all — Sos, Feb 17 '14 at 18:59
MapAt[# - 1 &, list, {All, 1}] or {#1 - 1, ##2} & @@@ list. — Artes, Feb 17 '14 at 19:01
Could you guys please post these as answers? Although they are somewhat redundant (given that they all should solve the problem), it is nice to see for others to see the various possibilities to solve this — Sos, Feb 17 '14 at 19:08
@Sosi I'm puzzled with the last line of the code list/.#[[1]]->/. #[[1]] & -> #[[1]] - 1 & doesn't work. What did you want to write? — Artes, Feb 18 '14 at 22:59
@Artes eheheh that was just a dumb idea on how I wanted it to work :P Also, I wanted to have written list/.#[[1]] & -> #[[1]] - 1 &. Maybe I should delete that part completely? — Sos, Feb 19 '14 at 09:40
Closely related: Elegant operations on matrix rows and columns and How to make MapAt work with Span? — Mr.Wizard, Apr 14 '14 at 22:17

score 16 · Accepted Answer · answered Feb 17 '14 at 19:14

16

You could use: MapAt:

MapAt[ # - 1 &, list, {All, 1}]

{{-1 + a, b, c, d}, {-1 + e, f, g, h}, {-1 + i, j, k, l}}

or Apply at the first level (shorthand @@@) (see also SlotSequence, shorthand ##n):

{#1 - 1, ##2}& @@@ list

answered Feb 17 '14 at 19:14

Artes

57,212
12
157
245

Your first answer, together with @andre's answer, seems to be the most robust since I can specify the position to to the subtraction, without having to do it only in the 1st position. – Sos Feb 18 '14 at 16:30

score 15 · Answer 2 · answered Feb 17 '14 at 19:33

15

This is quite neat:

list[[;; , 1]]--

answered Feb 17 '14 at 19:33

Kuba

136,707
13
279
740

2

It yields {a, e, i} for the list in the OP so one has to evaluate list twice to get the result of list /. {j_, k_, l_, m_} -> {j - 1, k, l, m}, since it changes list I find it's rather a drawback. – Artes Feb 18 '14 at 10:30
1

@Artes Indeed. Well, after this list is updated, the method you want to use depends of what OP needs at the end. – Kuba Feb 18 '14 at 10:33

score 7 · Answer 3 · answered Feb 17 '14 at 19:34

7

If you write

list[[All, 1]] = list[[All, 1]] - 1

list will be updated with the new values of the first element of each sublist.

answered Feb 17 '14 at 19:34

C. E.

70,533
6
140
264

andre314 · Answer 4 · 2014-02-17T20:08:05.277

6

Maybe

ReplacePart[list, (x : {_, 1}) :> (Extract[list, x] - 1)]

?

The positions of the elements are specified by the pattern on the indices : {_,1}

{{-1 + a, b, c, d}, {-1 + e, f, g, h}, {-1 + i, j, k, l}}

edited Feb 17 '14 at 20:08

answered Feb 17 '14 at 19:23

andre314

18,474
1
36
69

score 5 · Answer 5 · answered Dec 20 '23 at 23:47

5

That's a prime example to use Threaded which was introduced in v13.1

list = {{a, b, c, d}, {e, f, g, h}, {i, j, k, l}};
list + Threaded[{-1, 0, 0, 0}]

{{-1 + a, b, c, d}, {-1 + e, f, g, h}, {-1 + i, j, k, l}}

answered Dec 20 '23 at 23:47

bmf

15,157
2
26
63

2

+1 - That's probably the nicest solution – eldo Dec 20 '23 at 23:50
@eldo Thanks a lot :-) – bmf Dec 20 '23 at 23:53
1

(+1 ) I agree with @eldo, it seems like the nicest solution to me. :-) – E. Chan-López Dec 20 '23 at 23:56
@E.Chan-López thanks a lot mate :-) – bmf Dec 21 '23 at 00:02

m_goldberg · Answer 6 · 2014-02-17T19:33:46.737

5

You might be able to use this rule-based method

Replace[list, {f_, r___} -> {f - 1, r}, {1}]

{{-1 + a, b, c, d}, {-1 + e, f, g, h}, {-1 + i, j, k, l}}

or something similar. This will work for any sublist length.

list2 = {{a, b, c, d}, {e, f, g}, {h}};
Replace[list2, {f_, r___} -> {f - 1, r}, {1}]

{{-1 + a, b, c, d}, {-1 + e, f, g}, {-1 + h}}

More generally

munge[func_, data_] := Replace[data, {f_, r___} :> {func@f, r}, {1}]
munge[# - 1 &, list]

{{-1 + a, b, c, d}, {-1 + e, f, g, h}, {-1 + i, j, k, l}}

edited Feb 17 '14 at 19:33

answered Feb 17 '14 at 19:15

m_goldberg

107,779
16
103
257

I had been trying to play with replacement rules but to no avail, but now I see why. Btw, would there be a way to specify the position in which the replacement would have to be made? e.g. if I wanted to apply the rule to each element in position 37 of sublists with 100 elements? – Sos Feb 18 '14 at 16:26
Nevermind, I guess that would have to be something similar to what @andre answered – Sos Feb 18 '14 at 16:28

score 3 · Answer 7 · answered Dec 20 '23 at 16:56

list = {{a, b, c, d}, {e, f, g, h}, {i, j, k, l}};

We can also use ReplaceAt (new in 13.1)

ReplaceAt[x_ :> x - 1, {All, 1}] @ list

{{-1 + a, b, c, d}, {-1 + e, f, g, h}, {-1 + i, j, k, l}}

One of its advantages is that we can easily add conditions:

ReplaceAt[x_ /; x =!= e :> x - 1, {All, 1}] @ list

{{-1 + a, b, c, d}, {e, f, g, h}, {-1 + i, j, k, l}}

To update list inline we can employ ApplyTo (new in 12.2)

list //= ReplaceAt[x_ :> x - 1, {All, 1}];
list

{{-1 + a, b, c, d}, {-1 + e, f, g, h}, {-1 + i, j, k, l}}

E. Chan-López · Answer 8 · 2023-12-20T17:25:54.777

3

Using Cases:

list = {{a, b, c, d}, {e, f, g, h}, {i, j, k, l}};
Cases[list, x_ :> {-1 + First@x, Sequence @@ Rest@x}]
({{-1 + a, b, c, d}, {-1 + e, f, g, h}, {-1 + i, j, k, l}})

Edit Or as @eldo suggests, an equivalent way of doing it using Splice instead of Sequence:

Cases[list, x_ :> {-1 + First@x, Splice@Rest@x}] (*Thanks, eldo!*)
({{-1 + a, b, c, d}, {-1 + e, f, g, h}, {-1 + i, j, k, l}})

edited Dec 20 '23 at 17:25

answered Dec 20 '23 at 17:15

E. Chan-López

23,117
3
21
44

2

Very nice, +1, you could also use Splice@ instead of Sequence@@ – eldo Dec 20 '23 at 17:20

score 2 · Answer 9 · answered Dec 21 '23 at 09:24

2

list + ConstantArray[{-1,0,0,0},3]

(* {{-1+a,b,c,d},{-1+e,f,g,h},{-1+i,j,k,l}} *)

answered Dec 21 '23 at 09:24

user1066

17,923
3
31
49

1

That's, also, very slick! – bmf Dec 21 '23 at 09:53

score 0 · Answer 10 · answered Feb 20 '24 at 06:39

0

Using SubetMap:

Clear["Global`*"];
list = {{a, b, c, d}, {e, f, g, h}, {i, j, k, l}};
SubsetMap[# - 1 &, list, {All, 1}] // Column

Result:

answered Feb 20 '24 at 06:39

Syed

52,495
4
30
85

Subtracting from a specific column

10 Answers10

Linked

Related