1

Looking for a way to create an ErrorListPlot (x,y,error) with the radius of the PlotMarker determined by the magnitude of the error (which in my case is symmetrical), no actual error bars desired.

I want the size of the points to reflect the standard deviation of the datum, rather than Small,Largeor anyAbsolutePointSize` values.

I can probably approach this a variety of ways (BubbleChart, ListPlot with custom PlotMarkers, or ErrorListPlot with custom ErrorBarFunction) but I can't make progress. All of my efforts are being foiled by the relative scaling of PlotMarkers to the width of the plot, rather than the magnitude of the data values.

Kuba
  • 136,707
  • 13
  • 279
  • 740
Guest
  • 11
  • 1
  • 2
    It's very easy if you use Graphics and place a Disk at the data point with the standard deviation as the radius. Example: Graphics[Disk[{##2}, #/20] & @@@ RandomReal[1, {10, 3}]] Don't use PlotMarkers, as their sizing is fickle, as you realized. – rm -rf Feb 18 '14 at 06:39
  • Hello, ErrorBarFunction is not the case with relative scalling. Where did you stuck in this, could you share any code you want to improve? – Kuba Feb 18 '14 at 07:26

1 Answers1

3

Perhaps this (an example):

Needs["ErrorBarPlots`"]
ErrorListPlot[{{{1, 1}, ErrorBar[0.2, 0.3]}, {{2, 2}, 
   ErrorBar[0.2, 0.3]}, {{3, 4}, ErrorBar[0.2, 0.5]}, {{4, 8}, 
   ErrorBar[1, 2]}},
 ErrorBarFunction -> 
  Function[{coords, errs}, {Opacity[0.2], 
    Disk[coords, {(errs[[1, 2]] - errs[[1, 1]])/
       2, (errs[[2, 2]] - errs[[2, 1]])/2}]}], 
 PlotRange -> {{0, 6}, {0, 10}}, AspectRatio -> Automatic]

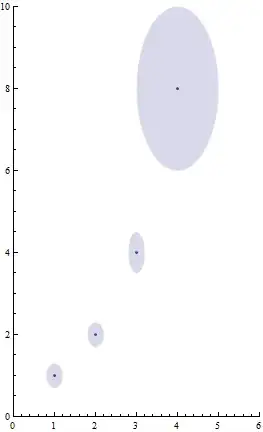
enter image description here

(aspect ratio to facilitate interpretation of error bars)

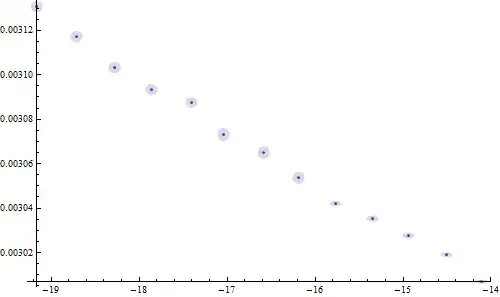
UPDATE As per request (and limited due to major time pressures): a quickly devised answer based on data provided. Note I accept aim is visualization of y uncertainty by size of blob but uncertainty in 'x' whatever x is suggested.

data = {{-19.1651, 0.00313089, 2.4711*10^-6}, {-18.7084, 0.00311717, 
    2.61428*10^-6}, {-18.2809, 0.00310325, 2.66765*10^-6}, {-17.8611, 
    0.00309356, 2.54845*10^-6}, {-17.4091, 0.00308763, 
    2.39272*10^-6}, {-17.0344, 0.00307304, 3.08935*10^-6}, {-16.5881, 
    0.00306513, 2.9771*10^-6}, {-16.1826, 0.00305374, 
    2.74635*10^-6}, {-15.7639, 0.00304204, 1.22568*10^-6}, {-15.3411, 
    0.00303553, 1.4538*10^-6}, {-14.9394, 0.00302755, 
    1.23145*10^-6}, {-14.5087, 0.00301919, 1.14451*10^-6}, {-14.1032, 
    0.00300701, 1.00403*10^-6}};
datam = {{#1, #2}, ErrorBar[0, #3]} & @@@ data;

ErrorListPlot[datam, 
 ErrorBarFunction -> 
  Function[{coords, errs}, {Opacity[0.2], 
    Disk[coords, {0.07, (errs[[2, 2]] - errs[[2, 1]])/2}]}], 
 ImageSize -> 500]

The $r_x$ size was a guess...you could customize...currently do not have time.

enter image description here

ubpdqn
  • 60,617
  • 3
  • 59
  • 148
  • Yes this is definitely it! However I'm having trouble getting this to work with my dataset, I'm confused by the radius calculations you are providing here (the subraction of 1std component from 2nd, halved). This seems unnecessary in my case so I dropped this portion. However I continue getting errors about the radius needing to be a positive number (which it is but is E-6). Do you think you could simply just get your script to work for my particular dataset? It's Yerror only, and not of form {{x,y},ErrorBar[err]} but rather {x,y,Yerr}. Thanks so much man! – Guest Feb 18 '14 at 18:51
  • {{-19.1651, 0.00313089, 2.471110^-6}, {-18.7084, 0.00311717, 2.6142810^-6}, {-18.2809, 0.00310325, 2.6676510^-6}, {-17.8611, 0.00309356, 2.5484510^-6}, {-17.4091, 0.00308763, 2.3927210^-6}, {-17.0344, 0.00307304, 3.0893510^-6}, {-16.5881, 0.00306513, 2.977110^-6}, {-16.1826, 0.00305374, 2.7463510^-6}, {-15.7639, 0.00304204, 1.2256810^-6}, {-15.3411, 0.00303553, 1.453810^-6}, {-14.9394, 0.00302755, 1.2314510^-6}, {-14.5087, 0.00301919, 1.1445110^-6}, {-14.1032, 0.00300701, 1.00403*10^-6}} – Guest Feb 18 '14 at 18:52
  • @Guest see update...am extremely time poor at present...hope is useful or you can adapt – ubpdqn Feb 19 '14 at 11:50
  • that is perfect. Any arbitrary but consistent value of x works, I just changed it to my actual uncertainty. Thanks greatly for the tips here, you've saved me quite a bit of face palming.

    One lesson I learned here was the use of #1, #2 and @@@ symbols in mathematica code. Call me a hack but I've never used this feature correctly. Previously I would have used something like below to generate your datam:

    datam = Table[{{xValues[[i]], yValues[[i]]}, ErrorBar[xValueError[[i]], yValueError[[i]]]}, {i, Length[xValues]}]

    where xValues,yValues, & errors are lists

    Thanks for the lesson!

     – Guest Feb 19 '14 at 20:31