Generating a (random) 2-dimensional cellular network

Question

I want to generate a network of random cells like the following picture:

The general idea is to generate some random points (x,y) as coordinate of a vertex and then randomly choose some of these points to connect them to achieve (almost) a random cellular network since there are two constraints:

1. The length of edges is constant.
2. Degree of each vertex is 3.

Thanks,

Update

I have been thinking about this problem for a while. Here's the conclusion:

By starting from a perfect honeycomb, we perform a series of random "neighbor switching" process:

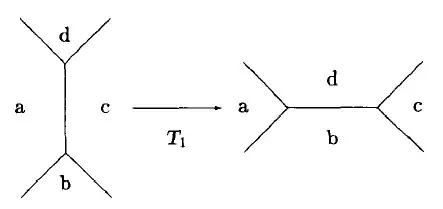
By performing successive neighbor switching, we are able to build cells with different size.

Answer 1

Fixing the edge length makes the problem harder. Otherwise, maybe this here gives an idea

<< ComputationalGeometry`
data = .9 Flatten[
    Table[{x, y} + .07 RandomReal[{-1, 1}, {2}], {x, -1, 
      1, .2}, {y, -1, 1, .2}], 1];
delval = DelaunayTriangulation[data];
convexHull = ConvexHull[data];
gr = DiagramPlot[data, ##, LabelPoints -> False] & @@ 
 BoundedDiagram[{{-1, -1}, {1, -1}, {1, 1}, {-1, 1}}, data, delval, 
  convexHull]

and further

gr /. {Point[___] :> Sequence[], 
  Line[pts_] :> ({EdgeForm[{Thick, Black}], 
     ColorData["Rainbow", RandomReal[]], Polygon[pts]})}