Generating a list of questions (simultaneous equations)

Question

I am trying to create a list of simultaneous equations showing steps, where I only need to change a, b and the question number, and maybe a couple of minor things about q (where q is the factored quadratic, and a & b are the integer factors). I am currently using:

a = -2; b = 1; q = 2 (a + x) (b + x);

q1 = Expand[q]; sol = x /. Solve[q1 == 0, x];
TraditionalForm[Grid[{{Grid[{{"2.       (1)      ", y, " = ", 
   If[Coefficient[q1, x, 2] == 1, "", Coefficient[q1, x, 2]], x, 
   If[Coefficient[q1, x, 1] > 0, "+", ""], Coefficient[q1, x, 1]},
  {"          (2)      ", x y, " = ", , -Coefficient[q1, x, 0], 
   " ", " ", " ", " ", " "}}]},{Grid[{{"       ", q1, "= 0"}}]},
{Grid[{{"          ", Factor[q1], "= 0"}}]},
{Grid[{{"{x,y} pairs:  ", {sol[[1]], 
    Coefficient[q1, x, 2]*sol[[1]] + Coefficient[q1, x, 1]}, 
   ",", {sol[[2]], 
    Coefficient[q1, x, 2]*sol[[2]] + Coefficient[q1, x, 1]}, " ", 
   " ", " ", " "}}]}}]]

which is a bit messy to say the least, but outputs:

enter image description here

not too far from the desired effect of:

$2.\quad\ \ \ (1)\quad \quad y=2x-2\\ \qquad \ \ (2)\quad \quad xy=4\\ \qquad \qquad\ \quad \ \ 2x^2-2x-4=0\\ \qquad \qquad \quad \ \ 2(x-2)(x+1)=0\\ \{x,y\}\text{ pairs: }\{-1,-4\},\{2,2\}$

though I should probably have used a table in my $\LaTeX$!

I am sure there is a better, more efficient way of doing this though.

Things I would like to improve: better spacing, automatic numbering, randomly chosen integer (or fraction) factors, random x sign changes, etc. (Basically a self-generating work/answersheet.)

Update

OK, I have replaced ubpdqn's top line with

q = RandomChoice[Join[Range[-5, -1], 
Range[1, 5]]] (RandomChoice[Join[Range
[-10, -1],  Range[1, 10]]] + x) 
RandomChoice[Join[Range[-10, -1], Range[1, 10]]]
+ x);
q1 = Expand[q];
sol = x /. Solve[q1 == 0, x];
eqn = {y == Coefficient[q1, x, 2] x - 
Coefficient[q1, x, 1], 
x y == -Coefficient[q1, x, 0]};

which generates question using random numbers, but have tried putting this into a table with n number of questions & just outputs same question n times :/ I suppose copy & paste will have to do for now...

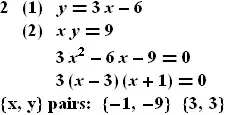
Could you add short explanation how a b and q are related to equations? It is in the code but it is not readable. p.s. I really see no reason to Solve[q1 == 0, x]. — Kuba, Mar 06 '14 at 10:21
OK - hope that is better. I wanted the expanded quadratic in the steps to solving the simultaneous equations. — martin, Mar 06 '14 at 10:25

score 3 · Answer 1 · edited Apr 13 '17 at 12:55

The answer by ybeltukov here may be very helpful.

Exploiting this (but not general):

eqn = {y == 2 x - 2, x y == 4}
Equations /: 
 MakeBoxes[Equations[eqs_, Alignment -> True], TraditionalForm] := 
 RowBox[{"\[Piecewise]", 
   MakeBoxes[#, TraditionalForm] &@
    Grid[{#1, "=", #2} & @@@ {##} & @@ eqs, 
     Alignment -> {{Right, Center, Left}}]}]

Module[{temp, sol, sol2, soln},
 temp = eqn[[2]] /. ReplacePart[eqn[[1]], 0 -> Rule];
 sol = temp /. x_ == y_ :> Expand[x] - y == 0;
 sol2 = Factor[sol[[1]]] == 0;
 soln = Column[Solve[eqn, {x, y}]];
 TraditionalForm[Style[Grid[{
     {"Equations", Equations[eqn, Alignment -> True]},
     {"Substition", sol},
     {"Factoring polynomial", sol2},
     {"Solutions", soln}
     }
    , Alignment -> {{Left, "="}, {Top, Automatic}}, Frame -> All], 20]]
 ]

enter image description here

UPDATE

Further to the comment by martin (but only generalizing to a,b as integers and not more generally and continuing to exploit code by ybeltukov):

func[a_, b_] := Module[{cl, pol, ans},
   pol[a, b] := 2 (x + a) (x + b);
   cl = CoefficientRules[pol[a, b], x];
   If[a == 0,
    ans = {y == x + b, x y == 0},
    If[b == 0,
     ans = {y == x + a, x y == 0},
     If[a + b == 0,
      ans = {y == x + b, x y == b^2 + b x} ,
      ans = {y == 
         FromCoefficientRules[
          cl[[1 ;; 2]] /. Rule[{x_}, y_] :> {x - 1} -> y, x], 
        x y == -2 a b}]]];
   ans];
Equations /: 
 MakeBoxes[Equations[eqs_, Alignment -> True], TraditionalForm] := 
 RowBox[{"\[Piecewise]", 
   MakeBoxes[#, TraditionalForm] &@
    Grid[{#1, "=", #2} & @@@ {##} & @@ eqs, 
     Alignment -> {{Right, Center, Left}}]}]

setup[eqn_] := Module[{temp, sol, sol2, soln},
  temp = eqn[[2]] /. ReplacePart[eqn[[1]], 0 -> Rule];
  sol = temp /. x_ == y_ :> Expand[x] - y == 0;
  sol2 = Factor[sol[[1]]] == 0;
  soln = Column[Solve[eqn, {x, y}]];
  Rasterize[TraditionalForm@Style[Grid[{
       {"Equations", Equations[eqn, Alignment -> True]},
       {"Substitution", sol},
       {"Factoring polynomial", sol2},
       {"Solutions", soln}
       }
      , Alignment -> {{Left, "="}, {Top, Automatic}}, Frame -> All], 
     20]]
  ]

Rasterize was required as TraditionalForm wrapper did not function in FlipView I apologise for the ugliness of conditionals dealing with exceptions of a=0 or b=o or a=-b.

Visualizing:

FlipView[setup[func @@ #] & /@ RandomInteger[{-5, 5}, {10, 2}]]

enter image description here

Great layout! Is there any way to use random numbers for a & b which will generate eqn, so only input would be number of questions? — martin, Mar 06 '14 at 10:58
@martin see update...not pretty but perhaps you can adapt to your needs — ubpdqn, Mar 06 '14 at 12:18
Yes, that's great :) - Can it be set up for a print environment? & generation of multiple equations for layout on a page? - I will have a play with your code - much appreciated :) — martin, Mar 06 '14 at 12:24
@martin I think it should be possible to take the objects and lay them out as you wish. Other more experienced users may be better able to assist the formatting. I suggest you experiment. If you hit a wall either update question (if minor) or ask another question related to particular problem. — ubpdqn, Mar 06 '14 at 12:32

Kuba · Answer 2 · 2014-03-06T10:34:19.807

1

Let's say you can deal with creating eq1 eq2 by yourself, here's what to do later:

a = 2;
b = -1;
eq1 = y == a x + a b
eq2 = x y == a^2

With[{subs = (eq2 /. Rule @@ eq1),
      sol = ({x, y} /. Solve[{eq1, eq2}, {x, y}])},
  Column[{
    Grid[{
      {"2", "(1)", eq1},
      {"", "(2)", eq2},
      {"", "", Expand[#1 - #2] == 0 & @@ subs},
      {"", "", Factor[#1 - #2] == 0 & @@ subs}
      }, Alignment -> Left]
    , Row[{"{x, y} pairs:", ## } & @@ sol, Spacer[5]]
    }, BaseStyle -> {18, Bold}]] // TraditionalForm

a = 1;
b = -2;

enter image description here

edited Mar 06 '14 at 10:34

answered Mar 06 '14 at 10:13

Kuba

136,707
13
279
740

Thanks - this really helps - with the spacing & generating of next question, etc. I would like to be able to generate an entire work/answersheet, using random integers / fractions for a & b. So input would be number of questions only. – martin Mar 06 '14 at 10:44
@martin I feel like I'm missing something from primary school about those steps between a b declaration and creation of equations (1) and (2). But I think it is not important here, it's more about output formating, right? – Kuba Mar 06 '14 at 10:45
The question will be only first two lines (1) & (2), but the question ensures integer / real factors if they are chosen from the start - no? – martin Mar 06 '14 at 10:50
The question I will give the students are the first two lines only. The rest is generation of hints / steps and answers. – martin Mar 06 '14 at 10:53
Would it be possible to generate an entire worksheet (using random seeds for example), and only having to input the number of questions desired? – martin Mar 06 '14 at 10:59
@martin You may use RandomInteger, make this grid a function and add there a button that will show more of the grid when at start it would be only two lines. – Kuba Mar 06 '14 at 11:03
That sounds great - could I make this printable, so by clicking the button, would print different things? – martin Mar 06 '14 at 11:05
@martin Please try to search the docs. Random/Button have many exaples and there is usualy easy to find function you don't know they exist by typing what do you expect. – Kuba Mar 06 '14 at 11:13
OK - thanks for your help - will do :) – martin Mar 06 '14 at 11:24

score 1 · Accepted Answer · answered Mar 07 '14 at 04:04

I am posting this update as a separate answer to avoid copy/paste issues wrt to similar codes. Once again this exploits ybeltukov's Equations code (see other answer).

func[a_, b_] := Module[{cl, pol, ans},
   pol[a, b] := 2 (x + a) (x + b);
   cl = CoefficientRules[pol[a, b], x];
   If[a == 0,
    ans = {y == x + b, x y == 0},
    If[b == 0,
     ans = {y == x + a, x y == 0},
     If[a + b == 0,
      ans = {y == x + b, x y == b^2 + b x} ,
      ans = {y == 
         FromCoefficientRules[
          cl[[1 ;; 2]] /. Rule[{x_}, y_] :> {x - 1} -> y, x], 
        x y == -2 a b}]]];
   ans];
Equations /: 
 MakeBoxes[Equations[eqs_, Alignment -> True], TraditionalForm] := 
 RowBox[{"\[Piecewise]", 
   MakeBoxes[#, TraditionalForm] &@
    Grid[{#1, "=", #2} & @@@ {##} & @@ eqs, 
     Alignment -> {{Right, Center, Left}}]}]

setupqa[eqn_] := Module[{temp, sol, sol2, soln, qst},
  temp = eqn[[2]] /. ReplacePart[eqn[[1]], 0 -> Rule];
  sol = temp /. x_ == y_ :> Expand[x] - y == 0;
  sol2 = Factor[sol[[1]]] == 0;
  soln = Column[Solve[eqn, {x, y}]];
  qst = Equations[eqn, Alignment -> True];
  {
   Rasterize[TraditionalForm[Style[qst, 20]]],
   Rasterize[TraditionalForm@Style[Grid[{
        {"Equations", qst},
        {"Substitution", sol},
        {"Factoring polynomial", sol2},
        {"Solutions", soln}
        }
       , Alignment -> {{Left, "="}, {Top, Automatic}}, Frame -> All], 
      20]]}
  ]

Setting up a set of 10 questions and answers:

{quest, ans} = 
  Transpose[setupqa[func @@ #] & /@ RandomInteger[{-5, -1}, {10, 2}]];

You can obviously choose whatever sample you want.

Creating question and answer notebooks:

qafun[comp_] := Grid[Thread[{TraditionalForm[Style[#, 20]] & /@ Range[1., 10., 1.], comp}], Alignment -> {Left, Top}];

qnb = DocumentNotebook[
   {TextCell[
     "Solve the following system of equations. Hint: use subsitution \
and polynomial factorization.\n", FontSize -> 20], qafun[quest]}];

anb = DocumentNotebook[
   {TextCell["Answers", FontSize -> 20], qafun[ans]}];

You can then save each notebook as pdf. This is just for motivation. I have not looked at page break issues or other style and formatting issues.

Example pdfs are here: questions, answers

The file sizes are not particularly economical (rasters). Perhaps exploiting TexForm` would be more efficient. Others would be better to advise.

@ ubpdqn, this is fantastic - just what I was after! I will experiment with the format / question types with this template. Thank you so much for your work on this :) — martin, Mar 07 '14 at 04:35
@martin just check equations solution make sense...was done in a rush...my main point is to point you to achieve what your aim is :) — ubpdqn, Mar 07 '14 at 04:39

Generating a list of questions (simultaneous equations)

Update

3 Answers3