Finding differences between Pi with varying number of decimals

Question

I have the following code

In[32]:= N[Pi, 2]

Out[32]= 3.1

In[33]:= N[Pi, 1]

Out[33]= 3.

In[34]:= N[Pi, 2] - N[Pi, 1]

Out[34]= 0.*10^-1

Why can't Mathematica find the difference between the two numbers?

Answer 1

N does not round numbers or truncate them.

The internal forms of

N[Pi, 1] // FullForm
N[Pi, 2] // FullForm

are respectively

(*
  3.1415926535897932384626433832795028842`1.
  3.1415926535897932384626433832795028842`2.
*)

Note that the numerical values are identical although the precisions differ. Their difference is zero and all significant digits are lost. The Front End typesets numerical results in StandardForm by showing only the significant digits determined by their precision.

This may be closer to what you're after:

Table[
 N[Floor[Pi, 10^n] - Floor[Pi, 10^(n + 1)]],
 {n, 0, -5, -1}]
(*
  {3.,
   0.1,
   0.04,
   0.001,
   0.0005,
   0.00009}
*)

---

Update to incorporate some of the related points made in the comments:

According to the tutorial NumericalPrecision, a nonzero approximate number x with precision p is defined to have uncertainty Abs[x] 10^-p. Likewise, the precision of a nonzero approximate number x with uncertainty d is given by -Log10[d/Abs[x]].

If approximate numbers are added or subtracted, the uncertainties are added. There are similar such rules for other arithmetic operations and the evaluation of functions. Consequently given two numbers $x_1,x_2$ with uncertainties $d_1,d_2$, the precision of $x_1\pm x_2$ is given by $$ p = -\log_{10}\left({d_1+d_2 \over |\,x_1\pm x_2|} \right)\,.$$

In the OP's case the precision would be negative (negative infinity at that). In cases where the precision is negative, Mathematica returns zero with corresponding computed accuracy.

Here is an illustration from the old comments. The function precDiff[{x1, p1}, {x2, p2}] computes the precision of the difference of numbers x1, x2 with precisions p1, p2.

precDiff[{x1_, p1_}, {x2_, p2_}] :=
   -Log10[(10^-p1 Abs[x1] + 10^-p2 Abs[x2])/Abs[x1 - x2]]

This shows that the computed precision of N[34/10, 2] - N[Pi, 1] is negative.

N @ precDiff[{34/10, 2}, {Pi, 1}]
N[34/10, 2] - N[Pi, 1] // FullForm
(*
  -0.129473
   0``0.4582220427094728
*)

This shows that the computed precision of N[35/10, 2] - N[Pi, 1] agrees with Mathematica's .

N @ precDiff[{35/10, 2}, {Pi, 1}]
N[35/10, 2] - N[Pi, 1] // FullForm
(*
  0.0113533
  0.35840734641020676153735661672049580005`0.011353331924907081
*)

Answer 2

Mathematica does not, by default, act like most calculators that will spew out digits in a result whether or not they are "valid" or "real" digits.

In most modes of usage, Mathematica keeps track of the precision of inputs, intermediate calculations, etc. and attempts to return results where the digits are correct, accurate, and "justified", that is, given a low-precision input applied to a high-precision input calculation, Mathematica will return results to the degree of precision warranted - you may better know this as significant digits. In fact, if you mouse-over the red box around the results you undoubtedly see, Mathematica will tell you what's going on "No significant digits are available to display."

You can see the effect of Mathematica's accuracy tracking by "forcing" the issue, e.g.:

8``1*8``1

returns

6.*10^1

instead of the 64 you might expect, because in the above example we've in essence told Mathematica the limits of the significance of our input.

Along with the manual control of such things, as alluded to earlier, Mathematica tracks how the values are used in calculations, and adjusts what is considered "significant" along the way to the end results, so they are displayed with no "false precision". You can observe this easily:

ListPlot[Accuracy /@ NestList[4 # (1 - #) &, 1/8`20, 20], Joined -> True]

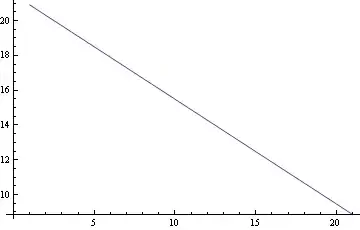
Note that as the repeated calculation progresses, using prior results to produce new ones, Mathematica adjusts the significance accordingly.

There is no better place to get the details than Mathematica's own documentation, e.g.:

Numbers (overview)

Precision and accuracy control

Exact and approximate results

Numerical evaluation and precision

How to control the precision and accuracy of numerical results

And a couple (of many) excellent posts at this very site :

Very different results...

When can I assume...