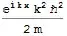I defined a one-dimensional momentum operator $\hat{p}=-i\hbar\frac{\partial}{\partial{x}}$ in Mathematica
p = -I * h * D[#, x]&
and I want to get the kinetic energy operator $\hat{T}=\hat{p}^2/2m=-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}$ from it, so
T = p^2/(2m)
but it gives the wrong result
What can I do about it? Do I have to derive the operators by hand?
Here is a more generalized method for what you want to do:
Let's define our momentum operator as you did above:
P := -I * h * D[#, x]&
Then we can define the nth power operator in a more general way as:
T[n_] := Nest[P, #, n] &
So for example the Kinetic energy operator (which is P^2 / (2 m)) will be:
T[2] / (2 m)
And we can use it on some function f as follows
(1/ (2 m))T[2]@(E^(I k x))
Which gives:
as expected.
Now if we want P^3 we just use T[3] etc.
You can't just squre an operator since no multiplication of functions (operators) are defined in Mathematica. You have to write something like
T = (p@p@#)/(2 m) &
or
T = p[p[#]]/(2 m) &
