the different way for a drunken man go back home in determined number of steps

Question

A drunken man walks in a two-dimensional grid.He can walk rigth(1),down(2),left(3),up(4).After determined number of steps,for example,6 steps,he has 400 ways go back home(the number of 1(2) equal to 3(4)，assume the number of 2(3) larger tan 1(3),then just 200 ways).

move = {1, 2, 3, 4};
AllWays[n_ /; EvenQ[n]] := {{1, 3} & /@ Range[#1], {2, 4} & /@ Range[#2]} & @@@
   PadLeft[IntegerPartitions[n/2, {0, 2}]] // Flatten /@ # & // Permutations /@ # & 
   // Join @@ # &

so if 6 steps,we will get:

{{2, 4, 2, 4, 2, 4}, {2, 4, 2, 4, 4, 2}, << 196 >>, {4, 2, 3, 1, 3, 1}, {4, 2, 3, 3, 1, 1}}

we can plot arrow pictures for this.

rule = {1 -> {1, 0}, 2 -> {0, -1}, 3 -> {-1, 0}, 4 -> {0, 1}};
handle[list_] := With[{n = Length[list] - 1},
    If[First[Subtract @@ #] == 0, 
      # + If[#[[1, 2]] < #[[2, 2]],{{0, 0.1}, {0, -0.1}}, {{0, -0.1}, {0,0.1}}], 
      # + If[#[[1, 1]] < #[[2, 1]], {{0.1, 0}, {-0.1, 0}}, {{-0.1, 0}, {0.1, 0}}]]
    & /@ (Transpose[{list,If[First[#2 - #1 & @@ First[list]] == 0,
     {{#, 0}, {#, 0}},{{0, #}, {0, #}}] & /@ Range[-0.05 n, 0.05 n, 0.1]}] 
     // Plus @@@ # &)]
ArrowPlot[moves_] := 
    Gather[Partition[Accumulate[moves /. rule], 2, 1, 1],Sort[#1] == Sort[#2] &] 
    //handle /@ # & // Flatten[#, 1] & 
    //Graphics[{Arrowheads[Medium], Arrow[#]}, ImageSize -> {70, 70}] &

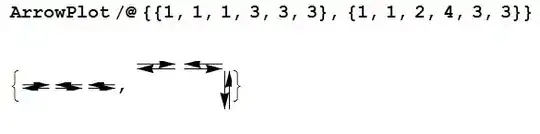
so ArrowPlot[{1, 1, 4, 2, 3, 2, 3, 4}] will get:

enter image description here

But there are three types of equivalence.

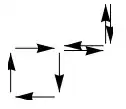
1.Topologically equivalence For example,{1, 2, 3, 4, 3, 4, 2, 1} is equal to {1, 2, 3, 4, 3, 2, 4, 1},because the images is

enter image description here

2.Translational equivalence For example,{1, 4, 1, 3, 3, 2} is equal to {4, 1, 3, 3, 2, 1},because they just have diffencnce origin,the images is

enter image description here

3.Rotate or reflect equivalence For example,{1, 4, 1, 3, 3, 2} is equal to {1, 2, 3, 2, 4, 4},because the images is

enter image description here

Obviously in 6 steps,Length[AllWays[6]] just equal to 200.It just has 7 difference ways,the images is

enter image description here

but in 8(10) steps,Length[AllWays[8(10)]] equal to 3710(31752).and the difference ways just equal to 20+(100+),how to write a program to tally those?

george2079 · Answer 1 · 2014-03-14T13:59:52.063

Here's a start -- note my first complete tuple list is larger that yours, i didn't sort out where the differece is.

n = 8;
(all = Select[ Tuples[ Range[4] , n], 
   Length[Cases[#, 2]] == Length[Cases[#, 4]] && 
      Length[Cases[#, 1]] == Length[Cases[#, 3]] & ]) // Length
cycmatch[a_, b_, n_] := ( 
      Position[  
            NestList[ Function[{list}, Permute[ list, Cycles[{Range[n]}]]] , 
                           a  , n ] , (b ) ] != {} );
(all = DeleteDuplicates[ all , cycmatch[#2, #1, n] &  ]) // Length    
(all = DeleteDuplicates[ all , 
         cycmatch[#2, #1 /. { 1 -> 3 , 3 -> 1}, n] &  ] ) // Length
(all = DeleteDuplicates[ all , 
         cycmatch[#2, #1 /. { 2 -> 4 , 4 -> 2}, n] &  ] ) // Length
(all = DeleteDuplicates[ all , 
         cycmatch[#2, #1 /. { 1 -> 2 , 2 -> 3, 3 -> 4 , 4 -> 1 } , n] &  ] ) // Length
(all = DeleteDuplicates[ all , 
         cycmatch[#2, #1 /. { 2 -> 1 , 1 -> 4, 4 -> 3 , 3 -> 2 }, n] &  ] ) // Length
(all = DeleteDuplicates[ all , 
         cycmatch[#2, #1 /. { 1 -> 3 , 2 -> 4, 3 -> 1 , 4 -> 2 },  n] &  ] ) // Length

4900 618 319 254 201 175 124

So we have 124 unique paths using only symmetry based matching:

 ArrowPlot[list_] := 
    Graphics[{Arrowheads[.3], 
      Arrow /@ Rest@FoldList[ { Last@#1 , Last@#1  +  Piecewise[
         {{ {1, 0} , #2 == 1} ,  {{0, -1} , #2 == 2} , 
         {{ -1, 0} , #2 == 3} , {{0, 1} , #2 == 4}  }  ]
            } & , {{0, 0}, {0, 0}}, list ]} ]

 GraphicsGrid[Map[ArrowPlot , Partition[all, 11] , {2}]]

enter image description here

Edit, considering 'reversed' paths to be eqivalent we are left with 93. Shown here sorted by the number of unique path elements:

enter image description here

Going further you need to clarify (mathematically) what you mean by topological equivalence.

score 0 · Answer 2 · answered Mar 13 '14 at 15:07

0

As it does not really matter the order in which the steps are performed, all you need to do is to sort the vector prior to tally. (It is the same {Left, Left, Up, Left) than {Up, Left, Left, Left}). Thus

Tally[Sort[#] & /@ AllWays[6]

answered Mar 13 '14 at 15:07

Zviovich

9,308
1
30
52

score 0 · Answer 3 · answered Mar 13 '14 at 15:15

For topologically equivalence,we can write a function.

toPoints[moves_] := With[{point = RotateRight@Accumulate[moves]}, 
  point /. Rule @@@ (Transpose[{#, Range[Length@#]}] &@DeleteDuplicates[point])]
Tally[AllWays[8], toPoints[#1 /. rule] == toPoints[#2 /. rule] &];

point is the trajectory.For example,{1,1,1,3,3,3}

In[33]= RotateRight@Accumulate[{1,1,1,3,3,3}/.rule]
Out[33]={{0,0}(*strat from origin*),{1,0}(*move right*),{2,0},{3,0},
       {2,0}(*move left*),{1,0}}

toPoints give the points move.so if two ways has the same trajectory,then they are topologically equivalence.

In[44]:= toPoints[{1,1,1,3,3,3}/.rule]
         toPoints[{1,1,2,4,3,3}/.rule]
Out[44]= {1,2,3,4,3,2}
Out[45]= {1,2,3,4,3,2}

so this two images are same to each ohter.

enter image description here

the different way for a drunken man go back home in determined number of steps

3 Answers3