Strange domain dependency with Maximize

Question

I'm using Mathematica 8 and strangely enough this code:

    Maximize[{x*(1-0.01 x),x>0},x,Integers]

produces the result {8.19,{x->9}}, which seems at odds with the actual answer of x->25.

Does anyone know if it is an intended behavior or my mistake?

Just for fun, try Maximize[{x*(1 - 0.01 x), x > 0}, x] :) — Dr. belisarius, Apr 18 '12 at 11:48

Dr. belisarius · Accepted Answer · 2012-04-18T19:11:19.943

15

As Szabolcs stated, Maximize is calling NMaximize.

The problem is that the call is not being done with appropriate options for your case. Just compare for example:

NMaximize[{x*(1 - 0.01 x), x ∈ Integers}, x]
(*
x-> 19
*)

with

NMaximize[{x*(1 - 0.01 x), x ∈ Integers}, x, MaxIterations -> 300]
(*
x-> 50
*)

To understand better what is happening you may see the evaluation process:

f[x_] := x*(1 - .01 x);
{sol, pts} = Reap[
   NMaximize[{f[x], x ∈ Integers}, x, MaxIterations -> 300,  
    EvaluationMonitor :> Sow[{x, f[x]}]]];
{sol1, pts1} = Reap[
   NMaximize[{f[x], x ∈ Integers}, x,  
    EvaluationMonitor :> Sow[{x, f[x]}]]];

GraphicsGrid[{{
   Plot[f[x], {x, 0, 100}, Epilog -> Map[Point, Cases[First[pts] , x_]]],
   Plot[f[x], {x, 0, 100}, Epilog -> Map[Point, Cases[First[pts1], x_]]]}}]

enter image description here

Edit

As Szabolcs commented below, the evaluation process is far from efficient. Here you have the number of evaluations done for each integer x while the algorithm is trying to find the Max:

Histogram[(First@pts1)[[All, 1]], {-1, 20, 1}, AxesLabel -> {"x", "# of evals"}]

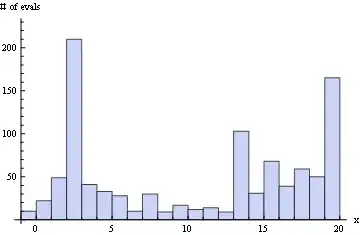
enter image description here

Edit

You could run

Histogram[Select[Length /@ Split@(First[pts1][[All, 1]]), # > 1 &]]

To see that it evaluates the same x several times is a row!

edited Apr 18 '12 at 19:11

answered Apr 18 '12 at 12:02

Dr. belisarius

115,881
13
203
453

Nice analysis! It is weird though that the function is called so many times with the same argument (the same elements appear many times in pts and pts1). If f is expensive to evaluate, this is really wasteful. – Szabolcs Apr 18 '12 at 12:29
It is better to evaluate NMaximize[{x*(1 - 0.01 x), x \[Element] Integers}, x, MaxIterations -> #] & /@ (50 Range[6]). It shows more details with messages generated. – Artes Apr 18 '12 at 12:49
@Szabolcs If that is the case, memoization could help – Dr. belisarius Apr 18 '12 at 13:21
@R.M Thanks for the edit – Dr. belisarius Apr 18 '12 at 15:01
@Szabolcs See edit – Dr. belisarius Apr 18 '12 at 15:59
Thanks, @belisarius! Will be using your convergence graphs very often. – iav Apr 20 '12 at 05:52

score 14 · Answer 2 · edited Apr 18 '12 at 14:41

You are using inexact numbers in the input (0.01). The documentation says that in this case Maximize will call NMaximize and will try to solve the problem using numerical methods. So your input is equivalent to

NMaximize[{x*(1 - 0.01 x), x > 0, x ∈ Integers}, x]

Here something goes wrong with the numerical method, and the returned answer is not correct.

Generally, when using functions that do symbolic operations, it is a good idea to only use exact numbers. The following input will give you the correct result:

Maximize[{x*(1 - 1/100 x), x > 0}, x, Integers]

(* ==> {25, {x -> 50}} *)

Generally, the function Rationalize is useful in converting expressions with lots of inexact numbers into exact ones. Try Rationalize[0.01].

Related reading:

The Uncertainties of Numerical Mathematics

Seems like the problem is not the numerical method, but the default number of iterations used by NMaximize[]. See my answer. It is easy to see what is happening by using EvaluationMonitor. — Dr. belisarius, Apr 18 '12 at 12:07

score 7 · Answer 3 · edited Apr 18 '12 at 15:41

7

Often NMaximize (which as others indicated is used behind the scenes) will work better if given some indication of a "useful" search space.

Realistic:

In[7]:= Maximize[{x*(1-0.01 x),100>x>0},x,Integers]
Out[7]= {25., {x -> 50}}

Too big:

In[8]:= Maximize[{x*(1-0.01 x),10000>x>0},x,Integers]
Out[8]= {4.75, {x -> 5}}

edited Apr 18 '12 at 15:41

Szabolcs

234,956
30
623
1,263

answered Apr 18 '12 at 15:32

Daniel Lichtblau

58,970
2
101
199

2

Do you know why NMaximize seems to evaluate the function for the very same argument many times, according to EvaluationMonitor? This happens also if I pass a "black-box" function to NMaximize and record the arguments passed to it inside the function (so it's not a problem with EvaluationMonitor): f[x_?NumericQ] := (Sow[x]; ...) This seems rather inefficient and it only happens when using x \[Element] Integers. – Szabolcs Apr 18 '12 at 16:04
2

There are two aspects to this. One is the work done in repeatedly evaluating a function at the same point. NMaximize et al do not memo-ize function evaluations (unless the definition of the function does that itself). The disadvantage is, as you observe, that reevaluations take place. The advantage is it rarely runs out of memory. The second issue is that it uses derivative-free methods that involve doing comparisons between old and new points (this happens with simulated annealing, differential evolution, and Nelder-Mead). So of necessity there will be reevaluations at points already visited. – Daniel Lichtblau Apr 18 '12 at 16:23
4

There you have a nice candidate for an option Memoize -> {True , False, N} – Dr. belisarius Apr 18 '12 at 16:33

Strange domain dependency with Maximize

3 Answers3