My simple model is:
m[t_] := m[t] = m[t - 1]*p + 2
m[0] = 0
p = 0.5
I can plot the system as:
DiscretePlot[m[t], {t, 0, 50}]
Now, I would like to shock p for a short period, say, from 10 to 13 during which it would be 0.8 and then recovering its original value, 0.5, afterwards. Would Insert do this?
No, Insert wouldn't work in your case because m[t] isn't a List. In your recursive definition, the "shock" can be incorporated directly as follows:
Clear[m];
m[t_] := m[t] = m[t - 1]*Piecewise[{{q, 10 <= t <= 13}, {p, True}}] + 2
m[0] = 0;
p = 0.5;
q = 0.8;
DiscretePlot[m[t], {t, 0, 50}, PlotRange -> All]
What I did is use Piecewise to decide whether to apply the factor p or q.
If[10 <= t <= 13,q, p] instead of Piecewise[{{q, 10 <= t <= 13}, {p, True}}]
– Murta
Mar 15 '14 at 23:29
As an alternative to Piecewise, you could construct a separate function for p using UnitStep. The modularity might provide more flexibility.
p[t_, shockAmplitudeDelta_, tBeginShock_, tEndShock_] := 0.5 + shockAmplitudeDelta(UnitStep[t - tBeginShock] -
UnitStep[t - tEndShock])
m[t_] := m[t] = m[t - 1]*p[t, 0.3, 10, 13] + 2
m[0] = 0;
DiscretePlot[m[t], {t, 0, 50}, PlotRange -> {0, 8}]
This provides the same DiscretePlot as Jens produced:
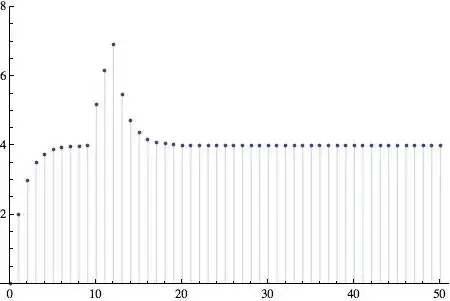
p[t_] /; 10 <= t <= 13 := 0.8; p[_] := 0.5. And usep[t]instead ofpin your definition ofm. But I don't understand the mathematical model. Could you explain it? – Michael E2 Mar 15 '14 at 20:13