As noted by previous answerers, the desired distributional properties of the spherical random walk were not properly clarified. Nevertheless, let me offer two variations of interest.
The first variation is the spherical analog of the bounded random walk (this recent thread shows a few ways on how to implement this). This would seem to have been the variation that was being attempted. Before I can show my solution, let me pull out a few auxiliary routines:
(* https://mathematica.stackexchange.com/a/10994 *)
arc[center_?VectorQ, {start_?VectorQ, end_?VectorQ}] := Module[{ang, co, r},
ang = VectorAngle[start - center, end - center];
co = Cos[ang/2]; r = EuclideanDistance[center, start];
BSplineCurve[{start, center + r/co Normalize[(start + end)/2 - center], end},
SplineDegree -> 2, SplineKnots -> {0, 0, 0, 1, 1, 1},
SplineWeights -> {1, co, 1}]]
(* slightly faster than the equivalent RotationMatrix[{vv1, vv2}];
from https://doi.org/10.1080/10867651.1999.10487509 *)
vectorRotate[vv1_?VectorQ, vv2_?VectorQ] :=
Module[{v1 = Normalize[vv1], v2 = Normalize[vv2], c, d, d1, d2, t1, t2},
d = v1.v2;
If[TrueQ[Chop[1 + d] == 0],
c = UnitVector[3, First[Ordering[Abs[v1], 1]]];
t1 = c - v1; t2 = c - v2; d1 = t1.t1; d2 = t2.t2;
IdentityMatrix[3] - 2 (Outer[Times, t2, t2]/d2 -
2 t2.t1 Outer[Times, t2, t1]/(d2 d1) + Outer[Times, t1, t1]/d1),
c = Cross[v1, v2];
d IdentityMatrix[3] + Outer[Times, c, c]/(1 + d) - LeviCivitaTensor[3].c]]
Here is a function that takes a bounded random step in the sphere.
boundedRandomStep[v_?VectorQ, φ_?NumericQ] :=
vectorRotate[{0, 0, 1}, v].({0, 0, Cos[φ]} +
Sin[φ] Append[Normalize[RandomVariate[NormalDistribution[], 2]], 0])
φ here is the length of the arc connecting the unit vector v and the generated random variate.
From this, here is how one might generate a bounded random walk:
With[{start = {0, 0, 1}, steps = 200, φ = π/15},
BlockRandom[SeedRandom[42, Method -> "Legacy"];
Graphics3D[{Sphere[], {Red, Sphere[start, Scaled[1/150]]},
{Directive[Blue, Arrowheads[Small]],
Arrow[Tube[arc[{0, 0, 0}, #], Scaled[1/1000]]] & /@
Partition[NestList[boundedRandomStep[#, φ] &, start, steps],
2, 1]}}, Boxed -> False, PlotRange -> 1.2]]]

Another variation rests on using a distribution biased towards a particular "mean direction"; one such distribution is the the von Mises-Fisher distribution. First, here is a routine for generating von Mises-Fisher variates (previously shown in this answer):
vonMisesFisherRandom[μ_?VectorQ, κ_?NumericQ] := Module[{ξ = RandomReal[], w},
w = 1 + (Log[ξ] + Log[1 + (1 - ξ) Exp[-2 κ]/ξ])/κ;
RotationTransform[{{0, 0, 1}, Normalize[μ]}][
Append[Sqrt[1 - w^2] Normalize[RandomVariate[NormalDistribution[], 2]], w]]]
Here is the random walk based on von Mises-Fisher:
With[{start = {0, 0, 1}, steps = 200, κ = 8},
BlockRandom[SeedRandom[42, Method -> "MersenneTwister"];
Graphics3D[{Sphere[], {Red, Sphere[start, Scaled[1/150]]},
{Directive[Blue, Arrowheads[Small]],
Arrow[Tube[arc[{0, 0, 0}, #], Scaled[1/1000]]] & /@
Partition[NestList[vonMisesFisherRandom[#, κ] &, start, steps],
2, 1]}}, Boxed -> False, PlotRange -> 1.2]]]



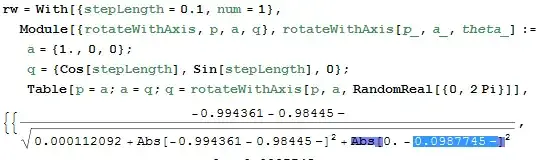



(1-Cos[theta])the minus is in fact\[Dash]. Just rewrite this expression and it should work. – Kuba Mar 22 '14 at 11:45#/Norm[#] &isNormalize. – Kuba Mar 22 '14 at 11:47\[Dash]to-. – Kuba Mar 22 '14 at 13:12\,[,D,... in Mathematica and got a dash, which is the opposite of your suggestion. I'm not sure she appreciates the difference between\[Dash]and\[Minus]that you're pointing out. – Michael E2 Mar 23 '14 at 13:43