How to use Undocumented Functions Prism, Tetrahedron and Hexahedron

Question

Taking a look at this question and this one, I checked to see if Mathematica really does not have a Prism primitive. To my surprise the function Prism was black but hitting the F1 key didn't bring up anything useful. I also stumbled upon Tetrahedron and Hexahedron as being undocumented too. So how can one properly use these functions? If these functions have already been unearthed please forgive me as I could not find any usage of them here.

Answer 1

I'll show some examples of using the undocumented function Prism. Tetrahedron and Hexahedron are very similar.

First some points:

g = {{4, 2, 4}, {2, 2, 2}, {6, 2, 2}, {4, 6, 4}, {2, 6, 2}, {6, 6, 2}}
p = Prism[g];

We can use p directly in Graphics3D e.g.

Graphics3D[p]

Or more fancy stuff:

Graphics3D[{EdgeForm[{Thick, Darker@Green}], 
  FaceForm[{Lighter@Yellow, Opacity[0.3]}], p}, Boxed -> False]

Doing ?Prism reveals it has the following Options

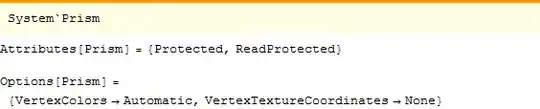
Edit

Here I show how to use Tetrahedron to generate a 3D Delaunay tetrahedralization:

First we load TeTGenLink package

Needs["TetGenLink`"]

Then we generate some points in 3D

pts3d = RandomReal[3, {50, 3}];

We tetrahedralize:

{ptstg, tetrahedra} = TetGenDelaunay[pts3d];
tetra = pts3d[[#]] & /@ tetrahedra;

Now the plot:

Graphics3D[{{Opacity[0.3], EdgeForm[{Thin, Darker@Blue}], 
   FaceForm[Yellow], Tetrahedron[tetra]}, {PointSize[0.02], Red, 
   Point[pts3d]}}, Boxed -> False, Lighting -> "Neutral"]

Will Be included in V10

As I was writing this up I looked online in the new Wolfram documentation and it turns out these functions will be officially included in the upcoming v10. If you want to see how Tetrahedron and Hexahedron are used please see here and here respectively. Note that some of the functionalities shown there are not implemented in current versions of Mathematica