Finding All Chordless Simple Cycles In A Graph

Question

I am doing a research on networks which consists of polygons with different number of sides. I am trying to find all simple cycles in a network which are chordless. As an example, consider the following graph:

graph = Graph[
  {
    1 <-> 2,   2 <-> 3,   3 <-> 4,  4 <-> 5,   5 <-> 6,   1 <-> 6,  
    3 <-> 7,   7 <-> 8,   8 <-> 9,  9 <-> 10, 10 <-> 11, 11 <-> 3,
    4 <-> 12, 12 <-> 13, 13 <-> 11
  }, 
    VertexLabels -> "Name"
]

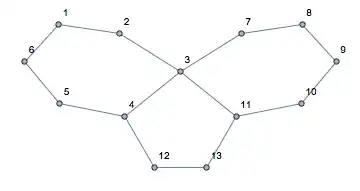
enter image description here

{1,2,3,4,5,6}, {3,4,11,12,13},{3,7,8,9,10,11} are rings and we can extract them:

cycles = FindFundamentalCycles[graph];
rings = Sort @* VertexList @* Graph /@ cycles

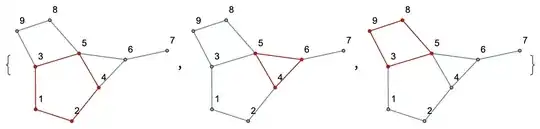
enter image description here

But the above solution doesn't always work as it might give non-chordless cycles. Consider the following example:

grapht = Graph[
{
  1 <-> 2, 1 <-> 3, 2 <-> 4, 4 <-> 5, 5 <-> 6, 4 <-> 6, 
  6 <-> 7, 3 <-> 5, 3 <-> 9, 5 <-> 8, 8 <-> 9
},
VertexLabels -> "Name"];

enter image description here

Rings (cycles) are:

cyclest = FindFundamentalCycles[grapht]; 
HighlightGraph[grapht, #] & /@ cyclest

enter image description here

But I need to get {4,5,6} as a ring not {1,2,3,4,5,6} since there is an edge in the latter. Is there any way to filter out only chordless cycles?

W Community crosspost

Greg Hurst · Answer 1 · 2019-12-18T17:16:01.227

9

Here's a weird way to find chordless cycles in V12+: convert the Graph into a Molecule and query for the set of smallest rings.

Your example:

grapht = Graph[
{
  1 <-> 2, 1 <-> 3, 2 <-> 4, 4 <-> 5, 5 <-> 6, 4 <-> 6, 
  6 <-> 7, 3 <-> 5, 3 <-> 9, 5 <-> 8, 8 <-> 9
},
VertexLabels -> "Name"];

rings = Molecule[grapht]["SmallestSetOfSmallestRings"]

{{1, 2, 4, 5, 3}, {6, 5, 4}, {8, 9, 3, 5}}

HighlightGraph[grapht, PathGraph[Append[#, First[#]]]] & /@ rings

Now it seems a graph with vertex degree greater than 4 can't become a molecule, but we can work around this with a hidden option. I've packed this into a function:

ChordlessRings[g_?GraphQ] :=
  Block[{mol, rings},
    mol = Quiet[Molecule[IndexGraph[g], "GraphValenceRules" -> {_ -> "C"}]];
    (
      rings = mol["SmallestSetOfSmallestRings"];

      rings /; ListQ[rings]

    ) /; MoleculeQ[mol]
  ]

ChordlessRings[___] = $Failed;

A larger example:

SeedRandom[4];
vm = VoronoiMesh[RandomReal[{-1, 1}, {100, 2}], {{-1, 1}, {-1, 1}}];
g = PlanarGraph[MeshCells[vm, 1][[All, 1]], VertexSize -> Large]

(rings = ChordlessRings[g]) // Length

HighlightGraph[g, PathGraph[Append[#, First[#]]]] & /@ rings[[1 ;; 5]]

Graphics @ GraphicsComplex[
  GraphEmbedding[g], 
  {EdgeForm[Black], {RandomColor[Hue[_]], Polygon[#]} & /@ rings}
]

Or we can ensure no 2 adjacent faces share the same color:

Block[{Print}, << IGraphM`]

imat = SparseArray[Join @@ MapIndexed[Thread[Thread[{First[#2], #1}] -> 1] &, rings]];
faceadj = Unitize[imat.Transpose[imat]];
faceconn = SimpleGraph@AdjacencyGraph[faceadj];

colors = IGMinimumVertexColoring[faceconn];

Graphics @ GraphicsComplex[
  GraphEmbedding[g], 
  {EdgeForm[Black], MapThread[{ColorData[112, #2], Polygon[#]} &, {rings, colors}]}
]

edited Dec 18 '19 at 17:16

answered Dec 17 '19 at 17:24

Greg Hurst

35,921
1
90
136

What's amusing about this solution is that it very likely uses an external method in RDKit which will probably then call back into a graph-theory library. Interesting the way the library calls chain. – b3m2a1 Dec 17 '19 at 22:34
In the Voronoi example you show, the outer face is also a chordless cycle, isn't it? But it's not returned by ChordlessRings. – Szabolcs Dec 18 '19 at 13:42
I don't think it is since there's edges inside, right? Or am I misunderstanding what chordless means? – Greg Hurst Dec 18 '19 at 13:44
Chordless means that none of the vertices of the cycle are directly connected by an edge (except those edges which are part of the cycle). Indirect connections are okay. Take e.g. WheelGraph[5]. It has a chordless 4-cycle. In other words, the subgraph induced by the vertices of the cycle is the cycle itself. – Szabolcs Dec 18 '19 at 13:46
Ah makes sense. And if the Voronoi graph were embedded in 3D not on a plane, it would be more evident that the outer cycle is such a cycle e.g. Graph3D[g, GraphLayout -> "HighDimensionalEmbedding"]. – Greg Hurst Dec 18 '19 at 13:49
1

I think I'll leave my answer though since I find the method amusingly absurd. – Greg Hurst Dec 18 '19 at 13:50
I think that the geometric view will always be misleading (it was also my mistake). If you imagine this graph embedded in a spherical surface, then the outer face is just a normal face. But it's not the only large chordless cycle. There will be many, many others. Here's another one: https://i.stack.imgur.com/K4SDN.png I think that there are so many that for this Voronoi graph it is not even feasible to list them all. – Szabolcs Dec 18 '19 at 13:54
I updated my answer to show the large number of solutions that exist. – Szabolcs Dec 18 '19 at 14:04
1

I am not sure what the exact definition of "SmallestSetOfSmallestRings" is, but I notice that the number of results it returns is the dimension of the cycle basis. So perhaps it finds a minimal cycle basis? – Szabolcs Dec 18 '19 at 14:05
Now, how to (in a simple way) color them all different colors, with no adjacent regions being the same color? I presume this is coloring each region randomly? It almost seems like the colorings are based on the number of sides for each region. Can you clarify this last point possibly? – CA Trevillian Dec 18 '19 at 15:45
1

@CATrevillian The coloring was just randomly chosen with RandomColor[Hue[_]]. I added an example showing a proper 4 coloring. See my latest edit. – Greg Hurst Dec 18 '19 at 17:17
BTW the next version of IGraph/M, if I ever get around to releasing it, won't need that annoying Block[{Print}, ...] anymore :) – Szabolcs Dec 18 '19 at 18:49

Szabolcs · Answer 2 · 2019-12-18T14:10:16.923

4

IGraph/M may help with this.

IGLADFindSubisomorphisms can look for induced subgraphs, and you are looking for induced cycles.

We can construct a function like this:

Needs["IGraphM`"]
chordlessCycles[graph_?UndirectedGraphQ] := 
  Join @@ Table[
    DeleteDuplicatesBy[Sort]@Values@IGLADFindSubisomorphisms[CycleGraph[k], graph, "Induced" -> True], 
    {k, IGGirth[graph], VertexCount[graph]}
  ]

This function will look for cycles of all sizes starting with the girth up to the vertex count. For your graph, it returns

chordlessCycles[graph]
(* {{3, 4, 12, 13, 11}, {1, 6, 5, 4, 3, 2}, {3, 7, 8, 9, 10, 11}} *)

Beware that in general there may be a very large number of induced cycles. Stealing Chip's graph generation code, here's an example:

SeedRandom[4];
vm = VoronoiMesh[RandomReal[{-1, 1}, {10, 2}], {{-1, 1}, {-1, 1}}];
g = PlanarGraph[MeshCells[vm, 1][[All, 1]], VertexSize -> Large]

cycle[vlist_] := PathGraph[Append[vlist, First[vlist]]]

HighlightGraph[g, cycle[#], GraphHighlightStyle -> "Thick", 
   ImageSize -> 60] & /@ chordlessCycles[g]

edited Dec 18 '19 at 14:10

answered Dec 17 '19 at 19:56

Szabolcs

234,956
30
623
1,263

2

I was going to use IGFaces but noticed it didn't find the 5 cycle in OP's problematic example, e.g. HighlightGraph[grapht, UndirectedEdge @@@ Partition[#, 2, 1, 1]] & /@ IGFaces[grapht]. Why is this? – Greg Hurst Dec 18 '19 at 12:53
@ChipHurst You're right, finding faces may not be a good method at all, perhaps unless the graph is planar and 3-vertex-connected, in which case its embedding is unique. This graph is not 3-connected, even after removing that dangling part. To get an idea of the embedding that IGraph/M is considering here, take a look at IGLayoutPlanar[grapht]. In that embedding, the 5 cycle is not a face. – Szabolcs Dec 18 '19 at 13:35
I removed the suggestion to use IGFaces. It was not a good one, for other reasons too: some chordless cycles cannot be faces in any embedding. – Szabolcs Dec 18 '19 at 13:36

score 4 · Accepted Answer · edited Apr 08 '15 at 20:33

First, let us find all cycles in the graph. Then, we will filter out the ones that contain chords; this we can detect by checking if the $n$-vertex induced subgraph is isomorphic to a cycle of length $n$ or not.

Let us use your graph as an example:

g = Graph[{1 <-> 2, 1 <-> 3, 2 <-> 4, 4 <-> 5, 5 <-> 6, 4 <-> 6, 
   6 <-> 7, 3 <-> 5, 3 <-> 9, 5 <-> 8, 8 <-> 9}, 
  VertexLabels -> "Name"];

cy = VertexList[Graph[#]] & /@ FindCycle[g, Infinity, All];
Select[cy, IsomorphicGraphQ[CycleGraph[Length[#]], Subgraph[g, #]] &]
(* {{4, 5, 6}, {5, 8, 9, 3}, {1, 2, 4, 5, 3}} *)

HighlightGraph[g, %]

Of course, if you have additional constraints, you can simply modify the call to FindCycle with different parameters to only find cycles of length e.g. of size 5, 6, 7, or 8. To achieve this, just do FindCycle[g, {5, 8}, All] instead.

Although, I found that this doesn't work in Mathematica 9 mostly because of FindCycle. — Mahdi, Apr 03 '15 at 05:59

Finding All Chordless Simple Cycles In A Graph

3 Answers3

Linked