How to get graph layout that reflects edge weights?

Question

My heart soared to discover that Mathematica 8 offers support for specifying a weighted adjacency matrix in WeightedAdjacencyGraph. But it seems that, regardless of the weights between edges, the plotted layouts of the graphs are the same.

For instance, the graphs produced here are the same:

adjMat1 = {{Infinity, 1, 1, 1, 1},
{1, Infinity, 1, 1, 1},
{1, 1, Infinity, 1, 1},
{1, 1, 1, Infinity, 1},
{1, 1, 1, 1, Infinity}};

adjMat2 = {{Infinity, 8, 6, 3, 7},
{1, Infinity, 1, 1, 1},
{2, 5, Infinity, 9, 4},
{1, 1, 1, Infinity, 1},
{1, 1, 1, 1, Infinity}};

WeightedAdjacencyGraph[adjMat1, DirectedEdges -> True]
WeightedAdjacencyGraph[adjMat2, DirectedEdges -> True]

I've tried specifying different layouts, but can't get them to display differently. Is there any way to get graphs with different edge weights but the same connectivity to render with the edge weights interpreted as distance between the nodes?

+1 I've had trouble with this too... It seems like the function is ineffective :/ — CHM, Apr 20 '12 at 02:00
VERY related http://stackoverflow.com/questions/7381085/how-to-label-graph-edges-with-their-weights — Dr. belisarius, Apr 20 '12 at 02:06
Yaroslav Bulatov's demo on multidimensional scaling may be a good place to start. — kglr, Apr 20 '12 at 03:06
My god these answers are fantastic -- not only answer the question, but go on to propose workarounds based on my intent. I am dumbfounded by the helpfulness of this community. — shanusmagnus, Apr 20 '12 at 16:32

DavidC · Answer 1 · 2012-04-20T15:54:20.577

Here's a way to represent the weights of the edges, first using GraphPlotand then Graph.

First, let's grab the edge weights from PlatoManiac's code and format them suitably for GraphPlot. (We'll use the unrasterized values.):

gr = WeightedAdjacencyGraph[adjMat2, DirectedEdges -> True];
weight = AbsoluteOptions[gr, EdgeWeight][[1, 2]];
edge = EdgeList@gr;
k = Graph[edge, EdgeLabels -> (el=MapThread[#1 -> #2 &, {edge, weight}])];
g = (AbsoluteOptions[k, 
  EdgeLabels] /. {(a_ \[DirectedEdge] b_ -> c_) :>  {a -> b, 
    c}})[[1, 2]];

GraphPlot

Now, making use of a technique illustrated here, let's make the thickness of the edges reflect the weights:

GraphPlot[g, 
   EdgeRenderingFunction -> ({Text[Style[#3, 15], Mean[#1]], Blue, 
   AbsoluteThickness[0.5 + #3/5], Arrowheads[0.02 + #3/170], 
   Arrow[#1, 0.075]} &), VertexLabeling -> True]

weighted graph

Graph

{e, w} = Transpose[g]
Graph[e, EdgeWeight -> w, 
EdgeLabelStyle -> Directive[Red, 20, Background -> White], 
EdgeLabels -> el , 
EdgeShapeFunction -> 
   el /. {((a_ \[DirectedEdge] b_) ->  c_) -> ((a \[DirectedEdge] 
    b) -> ({AbsoluteThickness[.9 + c/4], Arrow[#1, 0.025]} &))}]

graph 2

Thanks for the workaround, and for showing a different way to achieve the effect. — shanusmagnus, Apr 20 '12 at 16:35

score 13 · Accepted Answer · edited Apr 21 '17 at 11:20

Update: Since version 9, weighted layouts are available. See this answer.

The short answer is, unfortunately no, in version 8.0.* at least, the built-in layout algorithms do not take edge weight into account. Consider a version of your example:

Unweighted

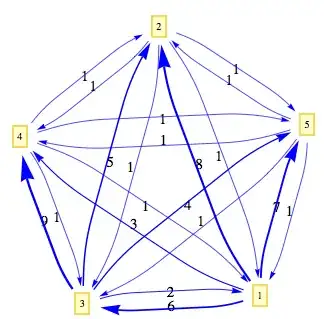
adjMat1 = {{Infinity, 1, 1, 1, 1}, {1, Infinity, 1, 1, 1}, {1, 1, 
    Infinity, 1, 1}, {1, 1, 1, Infinity, 1}, {1, 1, 1, 1, Infinity}};

Weighted

adjMat2 = {{Infinity, 8, 6, 3, 7}, {1, Infinity, 1, 1, 1}, {2, 5, 
    Infinity, 9, 4}, {1, 1, 1, Infinity, 1}, {1, 1, 1, 1, Infinity}};

Weighted adjacency matrix converted to multiedge rule form

multiedge = DeleteCases[ Flatten@Table[
    If[i == j, Null, Table[i -> j, {adjMat2[[i, j]]}]], {i, 
     Length[adjMat2]}, {j, Length@First@adjMat2}], Null]

(* Output:   {1 -> 2, 1 -> 2, 1 -> 2, 1 -> 2, 1 -> 2, 1 -> 2, 1 -> 2, 1 -> 2, 
 1 -> 3, 1 -> 3, 1 -> 3, 1 -> 3, 1 -> 3, 1 -> 3, 1 -> 4, 1 -> 4, 
 1 -> 4, 1 -> 5, 1 -> 5, 1 -> 5, 1 -> 5, 1 -> 5, 1 -> 5, 1 -> 5, 
 2 -> 1, 2 -> 3, 2 -> 4, 2 -> 5, 3 -> 1, 3 -> 1, 3 -> 2, 3 -> 2, 
 3 -> 2, 3 -> 2, 3 -> 2, 3 -> 4, 3 -> 4, 3 -> 4, 3 -> 4, 3 -> 4, 
 3 -> 4, 3 -> 4, 3 -> 4, 3 -> 4, 3 -> 5, 3 -> 5, 3 -> 5, 3 -> 5, 
 4 -> 1, 4 -> 2, 4 -> 3, 4 -> 5, 5 -> 1, 5 -> 2, 5 -> 3, 5 -> 4} *)

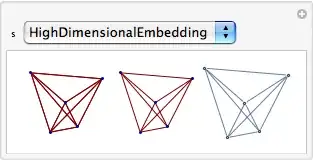
This shows that any of the three plotting methods give essentially the same layout for the same layout (Method/GraphLayout) option.

Manipulate[
 Row[{GraphPlot[multiedge, MultiedgeStyle -> None, Method -> s], 
   GraphPlot[adjMat1, MultiedgeStyle -> None, Method -> s], 
   AdjacencyGraph[adjMat1 /. \[Infinity] -> 0, 
    GraphLayout -> s]}], {s, {"SpringElectricalEmbedding", 
   "SpringEmbedding", "HighDimensionalEmbedding", "CircularEmbedding",
    "RandomEmbedding", "LinearEmbedding"}}]

enter image description here

If you were to come up with your own algorithm for allowing for the weights, you could draw graphs using that algorithm using the VertexCoordinateRules option.

There is a Weighted option in the GraphUtilities package, but it doesn't apply to visualisation.

Thanks. This answers exactly my question. – shanusmagnus Apr 20 '12 at 16:34 — shanusmagnus, Apr 20 '12 at 16:34

PlatoManiac · Answer 3 · 2012-04-20T14:43:38.217

Here is what you can do

Options[VisualizeNetwork] = Options[Graph];
VisualizeNetwork[{adjMat2_, edgecoloring_: {Green, Red}, 
scaling_: 600, opacity_: 0.5, ShowEdgeWeight_: True}, 
opts : OptionsPattern[]] :=
Block[{gr, weight, Nweight, edge, nodes, vertexStyle, EdgeBlendColor,edgeStyle, g},
gr = WeightedAdjacencyGraph[adjMat2, DirectedEdges -> True];
(*Lets extract the edge weight list from your graph object*)
weight = AbsoluteOptions[gr, EdgeWeight][[1, 2]];
(*Extract the edge list*)
edge = EdgeList@gr;
(*Extract the vertex list*)
nodes = VertexList@gr;
(* Make a color blend by scaling all the edge weight with the maximum edge weight *)
EdgeBlendColor = Map[ Blend[edgecoloring, #/Max[weight]] &, weight];
(* Make a thickness by scaling all the edge weight with the maximum edge weight *)
edgeStyle = 
MapThread[(#1 -> {Opacity[opacity], #3, 
     Thickness[#2/scaling]}) &, {edge, weight, EdgeBlendColor}];
Nweight = MapThread[
 Rasterize[#1, ImageSize -> 9, 
   Background -> Lighter@#2] &, {weight, EdgeBlendColor}];
 g = If[ShowEdgeWeight == True,
 Graph[nodes, edge, EdgeStyle -> edgeStyle, 
  EdgeLabels -> Flatten@MapThread[#1 -> #2 &, {edge, Nweight}], 
  VertexLabels -> 
   Table[i -> Placed["Name", {1/2, 1/2}], {i, nodes}], opts], 
 Graph[nodes, edge, EdgeStyle -> edgeStyle, 
  VertexLabels -> 
   Table[i -> Placed["Name", {1/2, 1/2}], {i, nodes}], opts]
 ];
g
];

You can call the function with all options available to Graph object and it returns a Mathematica 8.0 Graph object.Hence you don't need to call GraphPlot to tweak the visualization the default Graph object comes with this lay out where edge weight is evidently visible.

Given a weighted adjacency matrix it gives you the graph where you now see the edge weight in the lay out. We use color blend for edge color and control the edge thickness by scaling the all the edge weights by their maximum. There is also a True or False choice to show the edge weights explicitly or not.

adjMat1 = {{Infinity, 1, 1, 1, 1}, {1, Infinity, 1, 1, 1}, {1, 1, 
Infinity, 1, 1}, {1, 1, 1, Infinity, 1}, {1, 1, 1, 1, Infinity}};
adjMat2 = {{Infinity, 8, 6, 3, 7}, {1, Infinity, 1, 1, 1},
{2, 5,Infinity, 9, 4}, {1, 1, 1, Infinity, 1}, {1, 1, 1, 1, Infinity}};
(* Some Graph visualization option *)
opts = {VertexSize -> Medium, VertexSize -> Medium,
VertexStyle ->Directive[Opacity[0.65`], Blue, EdgeForm[None]], 
VertexLabelStyle -> Directive[GrayLevel[0], 12], 
VertexSize -> {"Scaled", 0.3`}, 
GraphLayout -> "SpringElectricalEmbedding"};
(* Call the function *)
GraphicsGrid@{{VisualizeNetwork[{adjMat1, {Yellow, Red}, 600, 0.5, 
 True}, opts], 
VisualizeNetwork[{adjMat2, {Yellow, Red}, 600, 0.5, True}, opts]}}

enter image description here

This doesn't really answer the question. The OP would like the layout of the graph to reflect the weight of the connection, i.e. for distances between nodes to be shorter, the higher the weight. I'm also interested in the answer. — Verbeia, Apr 20 '12 at 02:52
@Verbeia sorry for being inattentive while reading the actual question. I updated the solution. — PlatoManiac, Apr 20 '12 at 14:15
Thank you for taking the time to come up with this workaround. — shanusmagnus, Apr 20 '12 at 16:34

Szabolcs · Answer 4 · 2017-04-21T11:37:42.430

Some of the built-in layout algorithms can take weights into account since Mathematica version 9.

Graph[{1 <-> 2, 2 <-> 3}, EdgeWeight -> {1, 2}, 
 VertexLabels -> "Name", 
 GraphLayout -> {"SpringElectricalEmbedding", "EdgeWeighted" -> True}]

Mathematica graphics

It also works for "SpringEmbedding". Sub-options for graph layouts, such as "EdgeWeighted", are documented in the Scope section of the GraphLayout page.

With both layouts, a higher weight causes the vertices to be drawing further apart.

Alternatively, the IGraph/M package has a few layout algorithms that take weights into account.

<< IGraphM`
g = Graph[{1 <-> 2, 2 <-> 3}, EdgeWeight -> {1, 2}, VertexLabels -> "Name"];
IGLayoutFruchtermanReingold[g]

Mathematica graphics

Notice that with this layout, a higher weight causes the vertices to be drawn closer together.

I just tried this in V8 and the edge weights had no effect. Looks like this was new in 9. — Greg Hurst, Sep 30 '15 at 17:06

score 5 · Answer 5 · answered Nov 04 '15 at 20:52

5

Further to Szabolcs's post, EdgeWeight with SpringElectricalEmbedding works the opposite way to what you might expect. A weight of 2 results in an edge that is twice as long as for a weight of 1. In other words, the higher the weight, the weaker the spring and the more separation between the nodes. If you want a higher value to represent a stronger, shorter edge, you need to invert it, i.e. EdgeWeight -> 1/strength.

answered Nov 04 '15 at 20:52

Parsifal

136
2
2

I guess that depends on what you expect ... – Szabolcs Nov 05 '15 at 09:06
Thanks, I made this clearer in my answer. I think the spring is not weaker, just longer (two separate attributes). – Szabolcs Apr 21 '17 at 11:28

How to get graph layout that reflects edge weights?

5 Answers5

Linked

Related