Styling the edges of a graph according to the multiplicities of the edges

Question

I used the following code to make a simple triangle, in which the nodes have different effects each other:

data = {{0, 1, 0}, {0, 0, 2}, {3, 0, 0}};
AdjacencyGraph[data, VertexLabels -> "Name"]

That gave me three edges between nodes 1 and 3, and two edges between nodes 2 and 3. How can I show these multiplicities with edges that range from thin to thick.

---

@prgrad and @m_goldberg

I want to transform my graph into one which gives me single edge between the nodes. See the following picture:

for each different edge value of a different style. For example, for +3 dark black, for -3 dark red, etc.

Can you help to make a graph from my adjacency matrix that has these (minus and plus) labels?

Answer 1

If I understand your question correctly, you want the thickness of the edge to depend on the vertex the edge is directed towards?

If so, then you will need to use EdgeShapeFunction:

data = {{0, 1, 0}, {0, 0, 2}, {3, 0, 0}};
AdjacencyGraph[data, VertexLabels -> "Name",
EdgeShapeFunction ->
({
 Thickness[Last[#2]*0.01],
 Arrowheads[Sqrt[Last[#2]*0.01]],
 Arrow[#1]} &
)]

EdgeShapeFunction provides two parameters:

1. The coordinates of the vertices in the first argument #1, which is used to give the points between which the arrow should be drawn.
2. The name of the vertices between which the arrow is directed in the second argument #2. In this code I take the second value of #2 using Last[#2], that is the name of the vertex the arrow is going towards.

It is the second argument that allows us to define the thickness of the edge using Thickness. I multiply the vertex number by 0.01 to scale down the thickness to an appropriate size. I also have to define the size of the 'Arrowheads', and I find that taking the square of the values used for Thickness works well.

If you wanted to define the thickness according to the value of the vertex the edges are coming from you would use First[#2] rather than Last[#2].

Note also that the brackets () enclosing the EdgeShapeFunction list are important to making the code work. If I remember correctly this is because we are using DirectedEdges: see 'Possible Issues' in: http://reference.wolfram.com/language/ref/EdgeShapeFunction.html#

P

Answer 2

Taking into account the new information from your edit, I propose the following:

Function to produce the edge labels according to multiplicity indicated in the adjacency matrix.

 edgeLbl[multipliciy_] := 
   Style[StringJoin @ ConstantArray["+", multipliciy], Background -> White]

Function to style the edges according to multiplicity.

 edgeStyle[multipliciy_] := AbsoluteThickness[multipliciy]

My reason for defining these functions is to make it easy to modify the look of graph edges without having to modify the main graph making function, which is:

gr[adjMatrix_] :=
  Module[{m, edges, style, lbls},
   m = Map[Boole[# > 0] &, adjMatrix, {2}];
   edges = EdgeList @ AdjacencyGraph[m];
   style = Rule[#, edgeStyle[adjMatrix[[#[[1]], #[[2]]]]]] & /@ edges;
   lbls = Rule[#, edgeLbl[adjMatrix[[#[[1]], #[[2]]]]]] & /@ edges;
   AdjacencyGraph[m,
     EdgeStyle -> style,
     EdgeLabels -> lbls,
     VertexLabels -> "Name"]]
gr[{{0, 1, 0}, {0, 0, 2}, {3, 0, 0}}]

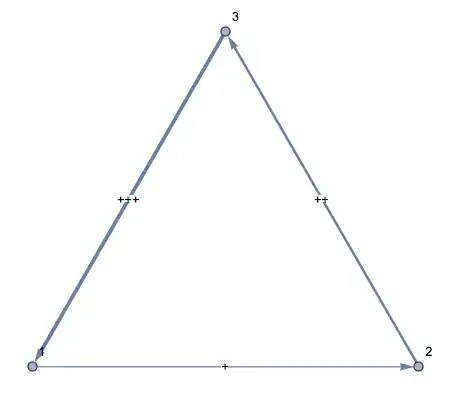
Update

The above doesn't adjust the size of the arrow heads according to the multiplicity. If you think that should happen, then a another function is needed.

arrow[multipliciy_] := 
  GraphElementData[{"FilledArrow", "ArrowSize" -> .018 + .01 multipliciy}]
gr[adjMatrix_] :=
  Module[{m, edges, style, arrows, lbls},
    m = Map[Boole[# > 0] &, adjMatrix, {2}];
    edges = EdgeList@AdjacencyGraph[m];
    style = Rule[#, edgeStyle[adjMatrix[[#[[1]], #[[2]]]]]] & /@ edges;
    lbls = Rule[#, edgeLbl[adjMatrix[[#[[1]], #[[2]]]]]] & /@ edges;
    arrows = Rule[#, arrow[adjMatrix[[#[[1]], #[[2]]]]]] & /@ edges;
    AdjacencyGraph[m,
      EdgeStyle -> style,
      EdgeLabels -> lbls,
      EdgeShapeFunction -> arrows,
      VertexLabels -> "Name"]]
gr[{{0, 1, 0}, {0, 0, 2}, {3, 0, 0}}]