Why does the filling on my ListPlot not reach the axis for some values?

Question

Why does

pPost[1, k_, p_: 2/3, p1_: 1/3, p2_: 2/3] := 
  (p p1^k (1 - p1)^(3 - k))/(p p1^k (1 - p1)^(3 - k) + (1 - p) p2^k (1 - p2)^(3 - k));
pPost[2, k_, p_: 2/3, p1_: 1/3, p2_: 2/3] := 
  ((1 - p) p2^k (1 - p2)^(3 - k))/(p p1^k (1 - p1)^(3 - k) + (1 - p) p2^k (1 - p2)^(3 - k));

Manipulate[
  Show[
    Plot[pPost[1, k, p, p1, p2], {k, 0, 3},
      PlotStyle -> {Dashed, Thin}, 
      PlotRange -> {All, {0, 1}}, 
      Ticks -> {{0, 1, 2, 3}, Automatic}],
    ListPlot[
      {{#, pPost[1, #, p, p1, p2]} & /@ Range[0, 3], 
       {#, pPost[2, #, p, p1, p2]} & /@ Range[0, 3]},
      PlotStyle -> {Green, Red}, 
      Filling -> Axis]],
  {{p, 2/3}, 0, 1},
  Delimiter,
  {{p1, 1/3}, 0, 1}, 
  {{p2, 2/3}, 0, 1}]

produce plots where the filling "disconnects" from the axis for some values of the Manipulate parameters?

Try p=0.75, p1=0.7, p2=0.6:

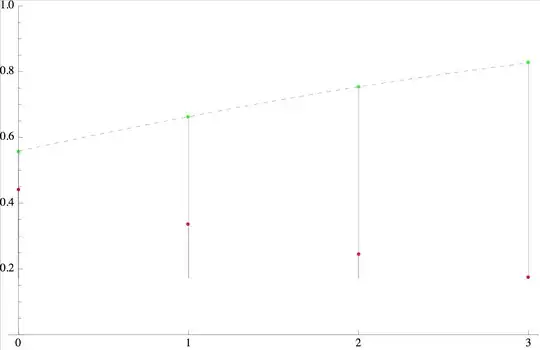
or (weirder) p=p1=p2=0.5

Didn't test but I suspect the Show. Set the final plot range in the ListPlot too, not just in Show, and set it to the same in all. Sorry if this doesn't help. — Szabolcs, Apr 05 '14 at 20:22
@Szabolcs: Setting PlotRange -> {All, {0, 1}} in ListPlot seems to do the trick. Where is the need for that documented? — orome, Apr 05 '14 at 20:40
I'm glad this helped. Sorry, I don't know where this is documented. What happens is that the lines are drawn only until the edge of the PlotRange. When you combine two graphics with Show, the PlotRange will be inherited from the first, so the filling lines for the second might not reach the frame edge. — Szabolcs, Apr 06 '14 at 00:55
Related: "Why does the order of arguments in Show influence the result?" — Alexey Popkov, Apr 06 '14 at 16:29
@Szabolcs: Thanks, that looks like an answer. (Still no sign of where this is documented; I bet it isn't, or at least not well.) — orome, Apr 06 '14 at 22:28
Ordering of options in Show is documented in its help page, both in the 'Details' section as well as the 'Possible Issues'section. — Sjoerd C. de Vries, Apr 23 '14 at 13:11

score 2 · Answer 1 · answered Apr 23 '14 at 10:32

While the order of the plots in Show makes difference, it is not the whole story. By default, many options are set automatically at the time of execution. In particular, PlotRange and AxesOrigin. The settings for Plot and ListPlot are determined separately since they are evaluated separately. This much I think can be inferred from the documentation, although not "easily."

When the ListPlot has a narrow plot height, the axes origin is moved up closer to the points. This can be controlled by setting PlotRange as mentioned in the comments. I would prefer to control it by setting

 AxesOrigin -> {0, 0}

in ListPlot to force the axes to always be at {0, 0}, and let the PlotRange be determined automatically.

Often in practice, to get two or more independent plots to look right when combined, automatically determined options often have to be set explicitly in all plots.

Why does the filling on my ListPlot not reach the axis for some values?

1 Answers1

Linked