We get different results because Simplify, working with a smaller range of accessible transformations than FullSimplify does, applied to structurally very different expressions at the begining, reaches only the local minimum of the default ComplexityFunction, being roughly close to LeafCount, unlike in case of FullSimplify even though its underlying ComplexityFunction may be the same.
Having defined :
bySum = Sum[k^2, {k, 1, n}];
byBernoulli = (BernoulliB[3, n + 1] - BernoulliB[3])/3;
we get :
bySum == byBernoulli // Simplify
True
because
Simplify[byBernoulli - bySum]
0
even though Simplify yields different results here :
{bySum, byBernoulli} // Simplify

This is because at the begining we have very different forms of the expressions which we can observe with help of TreeForm and LeafCount assessing the complexity :
LeafCount /@ { bySum, byBernoulli, byBernoulli - bySum }
{13, 26, 40}
TreeForm /@ {bySum, byBernoulli}

A kind of expression not involving special functions where FullSimplify simplifies it in a much better way than Simplify one can find here.
Knowing that algorithms behind FullSimplify contain a much wider range of transformations than Simplify the latter finds at certain stage only a local minimum (not sufficient in case of byBernoulli // Simplify to reach the global minimum) of the actual complexity function and therefore the resulting expressions are slightly different :
LeafCount /@ {bySum // Simplify, byBernoulli // Simplify}
{13, 15}
TreeForm /@ {bySum // Simplify, byBernoulli // Simplify}
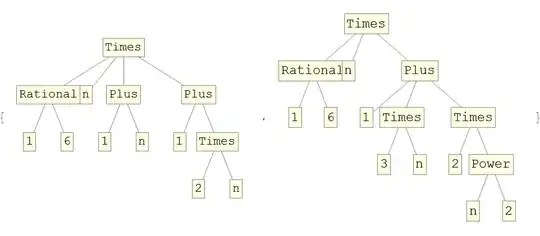
unlike in case of FullSimplify :
{bySum , byBernoulli } // FullSimplify
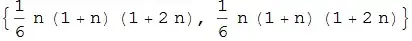
We needn't use FullSimplify to get the same expressions, a simpler solution of the problem would be this :
{bySum, byBernoulli} // Factor

which is the same as the result of FullSimplify for the both expressions as well as Simplify for bySum. It should be mentioned here, that FullSimplify when applied to a factorizable polynomials tends to give that polynomial in the factorized form, i.e. Factor[poly] yields by default its factorized form if poly is factorizable in the field of rationals, however if we extend the rationals appropriately the results will be different, e.g. Factor[1 - 10 x^2 + x^4, Extension -> {Sqrt[2], Sqrt[3]}] (see this answer). So this is rather a special case, a more genreal approach (also for polynomials not factorizable in the rationals)
would be :
{bySum, byBernoulli} // Collect[#, n] & // Simplify

The result is the same as in the case of byBernoulli // Simplify.



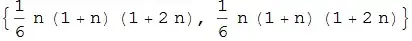


TreeFormand theLeafCount. See also sorting: http://mathematica.stackexchange.com/questions/2729/ordering-problem/2730 – tkott May 01 '12 at 00:37