Fraction of fibers that have failed

Question

I have the following to set into mathematica.

Assume a stress(sigma) applied on a specimen which has a number of fibers within it. All fibers that have a strength less than the applied stress should fail. I set a cumulative distribution of the fiber strengths with a mean and standard deviation.

I want to use this cumulative distribution to tell me how many fibers are less than the applied stress which have failed and store this number somewhere. This procedure should be repeated until all fibers have failed. so there is a convergence in the two variables. I am new in mathematica so sorry for a vague question.

thanks,

Nick

@blochwave. So far I have only trying to see how I should write it in mathematica but nothing in code yet — user10600, Apr 25 '14 at 13:56
I guess you want to loop until all fibers are gone. Keep them ordered by strength. Each iteration, select a random value from your probability distribution. If it exceeds the lowest remaining strength, remove fibers from there on until hitting one of adequate strength. Rinse, repeat. — Daniel Lichtblau, Apr 25 '14 at 14:16
Assume you are doing a simulation by generating a numerical list of strengths use Select. (You can do this analytically as well using CDF clarify if thats what you mean. ) — george2079, Apr 25 '14 at 14:30
@george2079 is it possible to put a normal distribution in the list from the select command? — user10600, Apr 25 '14 at 14:37
trying to give hints where to look in the docs.. the other thing you need is RandomVariate.. — george2079, Apr 25 '14 at 14:45

phosgene · Answer 1 · 2014-04-25T21:44:42.037

3

Here's an implementation showing the load-carrying capacity of the bundle of fibers as the weakest remaining fiber breaks:

nFibers = 1000;
mean = 100;
stdev = 20;
fibers = Sort@Abs@RandomVariate[NormalDistribution[mean, stdev], nFibers];
pull[{load_, fibers_}] := {
  First@fibers*Length@fibers,(* load just before weakest fiber breaks *)
  Rest@fibers(* remaining fibers after weakest fiber breaks *)
}
ListPlot[First@Transpose@NestList[pull, {0, fibers}, nFibers], Joined -> True]

enter image description here

The NestList command iteratively applies the 'pull' function, producing a sequence of the fiber bundle's load-carrying capacity as each successive fiber breaks.

edited Apr 25 '14 at 21:44

answered Apr 25 '14 at 18:53

phosgene

400
1
8

interesting approach. Note since you sorted the fibers it could be First@ instead of Min@ – george2079 Apr 25 '14 at 19:30
That's a good point. I'll change it to First@. – phosgene Apr 25 '14 at 21:08

george2079 · Answer 2 · 2014-04-28T16:50:19.920

Here is how you do this analytically: (using user2790167's pull in pure function form)

 nFibers = 50;
 mean = 100;
 stdev = 20;
 fibers = Sort@RandomVariate[NormalDistribution[mean, stdev], nFibers];
 Show[{
      Plot[  InverseCDF[ NormalDistribution[ mean, stdev] , nweak/nFibers] 
         (nFibers - nweak + 1 ), {nweak, 1, nFibers - 1}, PlotStyle -> {Red, Dashed}],
      ListPlot[
         Rest@First@
            Transpose@
              NestList[{First@#[[2]] Length@#[[2]], Rest@#[[2]]} &,
                  {0, fibers}, nFibers], Joined -> True, 
          AxesLabel -> {"Broken Fibers", "Net Load"}]}, PlotRange -> All, 
          AxesOrigin -> {0, 0}]

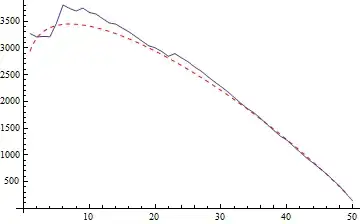
enter image description here

Also it is useful to plot against the strength of the fiber that is about to fail: (which correlates to strain assuming equal stiffness of the fibers )

 nFibers = 50;
 mean = 100;
 stdev = 20;
 fibers = Sort@RandomVariate[NormalDistribution[mean, stdev], nFibers];
 Show[{
   Plot[  s  (nFibers (1 - CDF[ NormalDistribution[ mean, stdev] , s]) ) ,
       {s, 0, 200}, PlotStyle -> {Red, Dashed}],
   ListPlot[
     First@
        Transpose@
           NestList[{{First@#[[2]] {1, Length@#[[2]]}, Rest@#[[2]]} &, 
             {{0, 0}, fibers}, nFibers], Joined -> True, 
           AxesLabel -> {"min surviving strength", "Net Load"}]}, PlotRange -> All, 
           AxesOrigin -> {0, 0}, AspectRatio -> 1/GoldenRatio]

enter image description here

for large nFibers the simulations converge to the analytic form..

Fraction of fibers that have failed

2 Answers2

Linked