Combining two plots with inverted xy-axes

Question

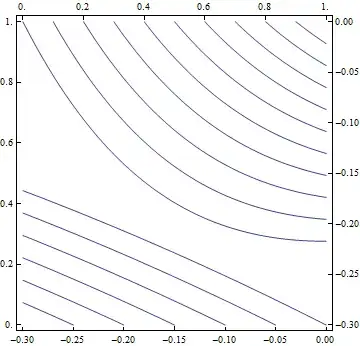
I need to draw a set of curves on one graph (characteristics equations). As you can see they have exchanged x and y axes. My goal is to plot all those curves on one graph. Are there ways to do that?

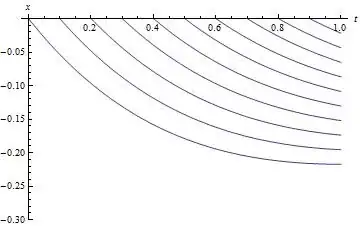
f[t_, t0_] := -(2 - 4/Pi*ArcTan[2])*Exp[-t]*(t - t0);
g[x_, x0_] := (x - x0)/(-(2 - 4/Pi*ArcTan[x + 2]));
Show[Table[Plot[f[t, t0], {t, 0, 1}, 
  PlotRange -> {0, -0.3}, 
  AxesLabel -> {t, x}], {t0, 0, 1, 0.1}]]

Show[
  Table[
    Plot[g[x, x0], {x, 0, -0.3}, PlotRange -> {0, 1}, AxesLabel -> {x, t}], 
    {x0, 0, -0.3, -0.05}]]

Answer 1

The problem boils down to "how to plot inverse function without explicit formula". You can use ParametricPlot[{h[y],y},{y...]:

Show[
 Plot[Table[f[t, t0], {t0, 0, 1, .1}], {t, 0, 1}, 
      Evaluated -> True, PlotStyle -> Blue],
 ParametricPlot[Table[{g[x, x0], x}, {x0, -0.3, 0, 0.05}], {x, -.3, 0}, 
                Evaluated -> True, PlotStyle -> Red]
 , 
 PlotRange -> {{0, 1}, {-.3, 0}}, Frame -> True, FrameLabel -> {"t", "x"}, 
 BaseStyle -> {18, Bold}]

Answer 2

Kuba's answer using ParametricPlot is the most convenient way to get the result you need. Alternatively, you can use a geometric transformation function that rotates and then reflects s2 around the vertical axis:

f[t_, t0_] := -(2 - 4/Pi*ArcTan[2])*Exp[-t]*(t - t0);
g[x_, x0_] := (x - x0)/(-(2 - 4/Pi*ArcTan[x + 2]));
s1 = Show[Table[Plot[f[t, t0], {t, 0, 1}, PlotRange -> {0, -0.3},
       AxesLabel -> {"t", "x"}, PlotStyle -> Red], {t0, 0, 1, 0.1}]];
s2 = Show[Table[Plot[g[x, x0], {x, 0, -0.3}, PlotRange -> {0, 1}, 
       AxesLabel -> {"x", "t"}], {x0, 0, -0.3, -0.05}]];

Define

trF = GeometricTransformation[#,
         Composition[ReflectionTransform[{-1, 0}], RotationTransform[Pi/2]]] &;

This transformation can be Apply'ed to s2

Show[s1, Graphics@(trF @@ s2)]

or MapAt'ed at position {1} of s2

Show[s1, MapAt[trF, s2, {1}]]

to get

Answer 3

Another way :

f[t_, t0_] := -(2 - 4/Pi*ArcTan[2])*Exp[-t]*(t - t0);
g[x_, x0_] := (x - x0)/(-(2 - 4/Pi*ArcTan[x + 2]));

curveset1 = Show[Table[ Plot[f[t, t0], {t, 0, 1}, PlotRange -> {0, -0.3}],
  {t0, 0, 1, 0.1}]] // First;
curveset2 = Show[Table[ Plot[g[x, x0], {x, 0, -0.3}, PlotRange -> {0, 1}],
  {x0, 0, -0.3, -0.05}]] // First;

Graphics[{
   GeometricTransformation[Scale[curveset1, {1, 10/3}, {0, 0}],
      TranslationTransform[{0, 1}]],
   GeometricTransformation[Scale[curveset2, {10/3, 1}, {0, 0}], 
      TranslationTransform[{1, 0}]]},
   Frame -> True, FrameTicks -> {#, Reverse@#} &@{Range[0, 1, 0.2],
     {#, NumberForm[N@(3/10) (# - 1), {5, 2}]} & /@ Range[0, 1, 1/6]}]