1

I have the following issue and can't find a solution so far.

t1 = 60.0*{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 
17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 
33, 34, 35, 36, 37, 38, 39, 40, 41, 42};
T11 = 273.15 + {17.0, 20.5, 22.5, 24.0, 25.5, 27.5, 29.0, 30.5, 32.0, 
33.0, 34.5, 36.0, 37.5, 39.0, 40.0, 41.5, 43.0, 44.0, 45.5, 47.0, 
48.0, 49.5, 50.5, 52.0, 53.0, 54.0, 55.5, 56.5, 57.5, 58.5, 59.5, 
61.0, 62.0, 63.0, 64.5, 65.5, 66.5, 67.5, 68.5, 69.5, 70.5, 71.0, 
72};
nlm1 = NonlinearModelFit[Transpose[{t1, T11}], 
a*x^2 + b*x + c, {a, b, c}, x, MaxIterations -> 1000];
T1[t_] = Piecewise[{{nlm1[t], t <= Max[t1]}, {nlm1[Max[t1]], 
 t >= Max[t1]}}];

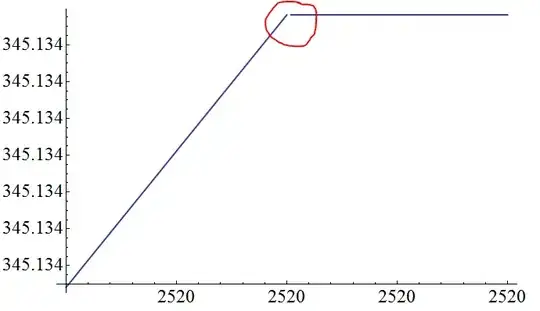
Then I plot a narrow segment of T1[t]:

Plot[T1[t], {t, 2519.9999, 2520.0001}]

(note that 60*42=2520)

and see this:

plot

This inconsistency leads to more badly inconsistencies in my other calculations.

I've tried to set Accuracy and Precision of initial data, those parameters of Piecewise function, WorkingPrecision, but with no result. Does anyone know how to solve this?

Community
  • 1
ApplMath
  • 71
  • 4

1 Answers1

1

Well, as @Öskå wrote, adding Exclusions -> None to Plot is all that was needed.

ApplMath
  • 71
  • 4