Model fitting to noisy data with a custom minimization function

Question

I'm looking into fitting some data with Mathematica. I've got my head around how NonlinearModelFit works (I've been using the Levenberg-Marquardt algorithm for some other work).

But my data this time is Poisson distributed, and I want to see if using the appropriate MLE for Poisson data is better for my scenario than nonlinear least squares fitting.

According to the paper Efficient Levenberg-Marquardt minimization of the maximum likelihood estimator for Poisson deviates, then the minimization for least-squares fitting, for data $y_{i}$ and the model $f_{i}$ is

$$ \chi^{2}=2\sum_{i=1}^{N} \frac{\left ( f_{i}-y_{i} \right )^{2}}{\sigma_{i}^{2}} $$

whereas for Poisson distributed data according to the paper, the minimization is

$$ \chi^{2}=2\sum_{i=1}^{N}f_{i}-y_{i}-2\sum_{i=1,y\neq 0}^{N}y_{i}\ln \left ( \frac{f_{i}}{y_i} \right ) $$

Is it possible to run a model-fitting in Mathematica using this minimization? And can a (modified?) Levenberg-Marquardt algorithm still be used?

Edit

There's an associated Nature Methods letter at http://dx.doi.org/10.1038/nmeth0510-338, with a revised version of the above link: http://www.nature.com/nmeth/journal/v7/n5/extref/nmeth0510-338-S1.pdf (courtesy of @belisarius)

Update #1

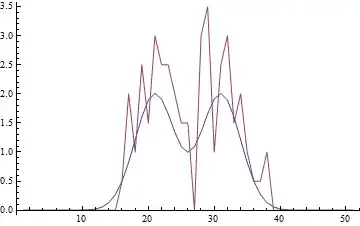
So here's the sort of data/model I'm looking to fit: the sum of two (or more) Gaussians, which may sometimes overlap as shown in the example below.

The amount of Poisson noise is deliberately significant as I'm dealing with very low counts. I've only posted a one-dimensional example here, but the data is in 2D, so there are more variables (x,y,means,heights,sigma...). I'm happy with using NonlinearModelFit to solve the problem, but I'm curious about dealing with the Poisson noise "more appropriately".

twoGaussianFunction[x_, A1_, sigma1_, mean1_, A2_, sigma2_, mean2_] := 
    A1 Exp[-((x - mean1)^2/(2 sigma1^2))] + 
    A2 Exp[-((x - mean2)^2/(2 sigma2^2))];

cleandata = Table[twoGaussianFunction[i, 10, 10, 30, 10, 10, 60], {i, 0, 100}];

noisydata = RandomVariate[PoissonDistribution[0.5 #]] & /@ cleandata;
ListLinePlot[{cleandata, noisydata}, PlotRange -> Full]

Answer 1

To answer my own question, I went with the suggestion by Oleksandr R:

Here I'm suggesting that you just write it directly as a minimization problem. In 4700, Ajasja and I did exactly this to perform a least squares fit using a custom minimizer, but you can of course minimize anything you want. By the way, you may also like to see GeneralizedLinearModelFit, which can be used for fitting Poisson-distributed data directly.

I ended up using NMinimize for my problem, rather than FindMinimum, but writing it as a minimisation problem was the solution. I used my Gaussian model as $f_{i}$ to solve for the data $y_{i}$ this:

$$ \chi^{2}=2\sum_{i=1}^{N}f_{i}-y_{i}-2\sum_{i=1,y\neq 0}^{N}y_{i}\ln \left ( \frac{f_{i}}{y_i} \right ) $$

as intended, with decent results.

First, the data:

twoGaussianFunction[x_, A1_, sigma1_, mean1_, A2_, sigma2_, mean2_] :=
   A1 Exp[-((x - mean1)^2/(2 sigma1^2))] + 
   A2 Exp[-((x - mean2)^2/(2 sigma2^2))];

cleandata = 
  Table[twoGaussianFunction[i, 2, 3, 20, 2, 3, 30], {i, 0, 50}];

noisydata = RandomVariate[PoissonDistribution[2 #]]/2 & /@ cleandata;

ListLinePlot[{cleandata, noisydata}, PlotRange -> Full, PlotLegends -> {"Original", "Noisy"}]

Then the minimisation function:

minimizeFunction[A1guess_, sigma1guess_, mean1guess_, A2guess_, 
   sigma2guess_, mean2guess_] := 
  2 Sum[twoGaussianFunction[i, A1guess, sigma1guess, mean1guess, 
       A2guess, sigma2guess, mean2guess] - noisydata[[i]], {i, 50}] - 
   2 Sum[If[noisydata[[i]] == 0., 0,noisydata[[i]]*
       Log[twoGaussianFunction[i, A1guess, sigma1guess, mean1guess, 
          A2guess, sigma2guess, mean2guess]/noisydata[[i]]]], {i,50}];

Followed by NMinimize:

bestfit = 
  NMinimize[{minimizeFunction[a, b, c, d, e, f], 
    a > 0 && b > 0 && c > 0 && d > 0 && e > 0 && f > 0},
   {{a, 1, 3},
    {b, 2, 4},
    {c, 15, 25},
    {d, 1, 3},
    {e, 2, 4},
    {f, 25, 35}},
   Method -> "NelderMead",
   MaxIterations -> 100
   ];

cleaneddata = 
  Table[twoGaussianFunction[i, a /. Last[bestfit], b /. Last[bestfit],
     c /. Last[bestfit], d /. Last[bestfit], e /. Last[bestfit], 
    f /. Last[bestfit]], {i, 1, 50}];

ListLinePlot[{cleandata, cleaneddata}, PlotRange -> Full, 
 PlotLegends -> {"Original", "Fitted"}]

There's probably room for improvement in the way I've implemented it - certainly for speed, perhaps using Parallelize in the minimisation function? (That was my first thought). I've still got to test it fully against the standard least-squares method though...