19

Bug introduced in 9 and fixed in 11.1

I get a hit on performance with the Exp function depending on the range of my inputs. for example, with:

w1 = RandomComplex[-20000 I, {10000000}];
Exp[w1]; // Timing

w2 = RandomComplex[-20 I, {10000000}];
Exp[w2]; // Timing

Results in 2.4 and 0.4 sec respectively. What mystifies me is that the involved numbers are not in a numerically "interesting" range.

The transition to slower times starts gradually at about -500 I and asymptotically stabilizes by about -10000 I. Past these ranges the timings are stable:

w = RandomComplex[-I, {1000000}];
t = Table[{10^n, Timing[Exp[10^n w]][[1]]}, {n, 1.5, 5, .01}];
ListLogLinearPlot[t, AxesLabel -> {"Scaling", "Time"}]

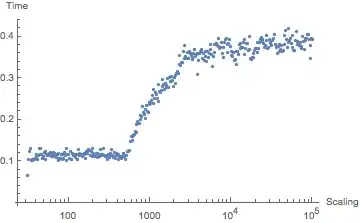
Any ideas what might be happening here? Any simple fixes to get faster performance with high scaling factors?

Alexey Popkov
  • 61,809
  • 7
  • 149
  • 368
user173743
  • 331
  • 1
  • 2
  • You could try writing it explicitly in terms of Sin/Cos. – Szabolcs May 16 '14 at 17:56
  • Yes, but that is much slower for the smaller range inputs. Plus having readable code might be nice! – user173743 May 16 '14 at 18:12
  • 1
    I do not see this effect in version 8.0.4 on OS X. Both timings are about the same (to within three digits), and the timing plot shows just an increase in the variance of the timings, not really a trend. All times in the plot are below .066 on my computer. – Jens May 16 '14 at 18:20
  • I don't see this effect either running 9.0.1 on Win8.1 – dr.blochwave May 16 '14 at 18:23
  • I don't see it either in v8.0.4 on Linux. – Öskå May 16 '14 at 18:26
  • I'm getting this on 9.0.1 on a Mac. Maybe it is a platform specific issue ... – user173743 May 16 '14 at 18:35
  • 1
    I do see this on OS X/M9.0.1 to a great extent on one computer, to a smaller one on another. I don't see it on OSX/M8.0.4. I do see it on Windows8/M9.0.1. I do see it on Ubuntu 14.04/M9.0.1. Performance is much better on Windows (despite running in VirtualBox) than on Mac/Linux (nearly 3x better) despite running on the same machine. CPU is "Intel(R) Core(TM) i7-3720QM CPU @ 2.60GHz". – Szabolcs May 16 '14 at 18:48
  • I see something similar though much more stratified (link). Win7-64 M9.0.1. – Sjoerd C. de Vries May 16 '14 at 18:51
  • You might want to increase the length of w, the runs are too short and the timer is quantized (or is there a higher precision timer in Mathematica?) – user173743 May 16 '14 at 18:52
  • @user173743 Mathematica's timer precision is determined by the OS. It's 15 ms on WinXP and better elsewhere (up to 1 ms resolution depending on platform). Do not trust $TimeUnit (it's typically incorrect). – Szabolcs May 16 '14 at 18:58
  • @user173743 It sounds like it would benefit us all if you reported these findings to Wolfram Support. – Szabolcs May 16 '14 at 19:06
  • Ok, will do. Just making sure that I wasn't missing anything obvious. – user173743 May 16 '14 at 19:34
  • 1
    It appears that Exp[I x] slows down for Abs[x] >= 512. The transition is clearer like this: w = ConstantArray[N[I], {5000000}]; t = Table[{n, Timing[Exp[n w]][[1]]}, {n, 510, 514, 0.1}] – Simon Woods May 17 '14 at 13:14
  • Possibly related: Slow exponential evaluation over lists – Karsten7 Mar 18 '15 at 00:06
  • Using a numerical version nExp of Exp similar to my answer to Slow exponential evaluation over lists, but with _Complex instead of _Real inside Compile I only get the long timings independent of Scaling. Plot – Karsten7 Mar 18 '15 at 02:18
  • 2
    @SimonWoods:Interesting find! A similar step then happens at 2^30 (and then not until 2^100 where I stopped measuring). I suppose that's where Mathematica "shifts gears" – takes on a different algorithm. With the OP's case it can then be seen that for 10^n < 512, all the random numbers are within the safe interval. For larger n, some of them overflow 512 I and the new algorithm is only used for those. For a much larger value, almost all of them are higher than 512 so MMA is using the slower approach for almost each of the 10^7 numbers, resulting in levelling of the time at a new value. – The Vee Jun 12 '16 at 00:33

1 Answers1

4

This bug has been fixed in the just released Mathematica 11.1.

w1 = RandomComplex[-20000 I, {10000000}];
AbsoluteTiming[Exp[w1];]

w2 = RandomComplex[-20 I, {10000000}];
AbsoluteTiming[Exp[w2];]

(* {0.126897, Null} *)
(* {0.123388, Null} *)
ilian
  • 25,474
  • 4
  • 117
  • 186